Holstein MPO
\[\begin{split}\sum_{i=1}^{3}
\begin{bmatrix}
\frac{\omega}{2}\left(p_i^2+q_i^2\right) & \lambda q_i \\
\lambda q_i & \frac{\omega}{2}\left(p_i^2+q_i^2\right)+ \kappa q_i
\end{bmatrix}
+
\begin{bmatrix}
0 & J \\
J & \Delta E
\end{bmatrix}\end{split}\]
[1]:
import numpy as np
import sympy
from pympo import (
AssignManager,
OpSite,
SumOfProducts,
)
[2]:
Holstein = SumOfProducts()
omega = sympy.Symbol("omega")
lam = sympy.Symbol("lambda")
kappa = sympy.Symbol("kappa")
ΔE = sympy.Symbol(r"\Delta E")
J = sympy.Symbol("J")
ndim = 4
ints_p2 = np.ones((3, 3))
ints_q = np.ones((3,))
ints_q2 = np.ones((3,))
p2_ops = [OpSite(r"\hat{p}^2" + f"_{i}", i, value=ints_p2) for i in range(ndim)]
q2_ops = [OpSite(r"\hat{q}^2" + f"_{i}", i, value=ints_q2) for i in range(ndim)]
q_ops = [OpSite(r"\hat{q}" + f"_{i}", i, value=ints_q) for i in range(ndim)]
# Electronic states are second-quantized
adag_op = np.zeros((2, 2))
adag_op[0, 1] = 1.0
adag_ops = [OpSite(r"\hat{a}^\dagger" + f"_{i}", i, value=adag_op) for i in range(ndim)] # creation
a_op = np.zeros((2, 2))
a_op[1, 0] = 1.0
a_ops = [OpSite(r"\hat{a}" + f"_{i}", i, value=a_op) for i in range(ndim)] # annihilation
[3]:
a_dim = 3 # estate-mode
b_dim = set([0, 1, 2, 3]) - set([a_dim]) # bath-mode
for i in b_dim:
Holstein += (omega / 2 * (p2_ops[i] + q2_ops[i])) * a_ops[a_dim] * adag_ops[a_dim]
Holstein += (omega / 2 * (p2_ops[i] + q2_ops[i])) * adag_ops[a_dim] * a_ops[a_dim]
Holstein += (kappa * (q_ops[i])) * adag_ops[a_dim] * a_ops[a_dim]
Holstein += (lam * q_ops[i]) * a_ops[a_dim]
Holstein += (lam * q_ops[i]) * adag_ops[a_dim]
# Holstein += (lam * q_ops[i]) * (adag_ops[a_dim] + a_ops[a_dim]) # can also work.
Holstein += ΔE * adag_ops[a_dim] * a_ops[a_dim]
Holstein += J * (adag_ops[ndim-1] + a_ops[ndim-1])
# Following setting also works instead of above line.
# Holstein += J * a_ops[a_dim]
# Holstein += J * adag_ops[a_dim]
Holstein = Holstein.simplify() # This method find concatenatable operator in advance like q_i*a_j + q_i*a†_j = q_i * (a_j+a†_j)
display(Holstein.symbol)
$\displaystyle J \left(\hat{a}^\dagger_3 + \hat{a}_3\right) + \Delta E \hat{a}^\dagger_3 \hat{a}_3 + \kappa \hat{q}_0 \hat{a}^\dagger_3 \hat{a}_3 + \kappa \hat{q}_1 \hat{a}^\dagger_3 \hat{a}_3 + \kappa \hat{q}_2 \hat{a}^\dagger_3 \hat{a}_3 + \lambda \hat{q}_0 \left(\hat{a}^\dagger_3 + \hat{a}_3\right) + \lambda \hat{q}_1 \left(\hat{a}^\dagger_3 + \hat{a}_3\right) + \lambda \hat{q}_2 \left(\hat{a}^\dagger_3 + \hat{a}_3\right) + \frac{\omega \left(\hat{p}^2_0 + \hat{q}^2_0\right) \hat{a}^\dagger_3 \hat{a}_3}{2} + \frac{\omega \left(\hat{p}^2_0 + \hat{q}^2_0\right) \hat{a}_3 \hat{a}^\dagger_3}{2} + \frac{\omega \left(\hat{p}^2_1 + \hat{q}^2_1\right) \hat{a}^\dagger_3 \hat{a}_3}{2} + \frac{\omega \left(\hat{p}^2_1 + \hat{q}^2_1\right) \hat{a}_3 \hat{a}^\dagger_3}{2} + \frac{\omega \left(\hat{p}^2_2 + \hat{q}^2_2\right) \hat{a}^\dagger_3 \hat{a}_3}{2} + \frac{\omega \left(\hat{p}^2_2 + \hat{q}^2_2\right) \hat{a}_3 \hat{a}^\dagger_3}{2}$
[4]:
from pympo import (
OpSite,
SumOfProducts,
assign_core,
get_UVE,
show_assigns,
show_bipartite,
show_maximal_matching,
show_min_vertex_cover,
)
Hamiltonian = Holstein
W_assigns: list[list[int]] = [
[k for _ in range(Hamiltonian.ndim)] for k in range(Hamiltonian.nops)
]
coef_site: list[int] = [Hamiltonian.ndim - 1 for _ in range(Hamiltonian.nops)]
W: list[sympy.Basic] = []
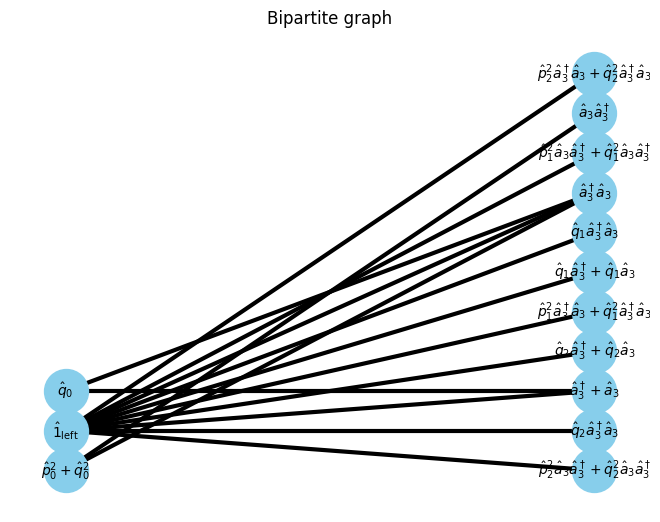
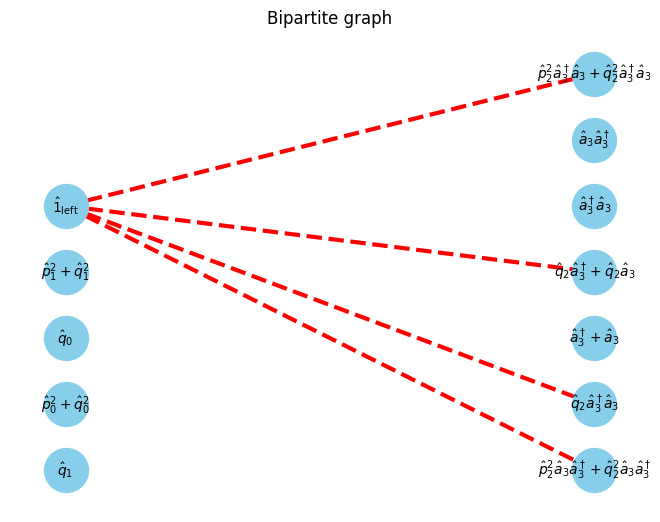
U, V, E, E_assigns = get_UVE(Hamiltonian, W_assigns, 0)
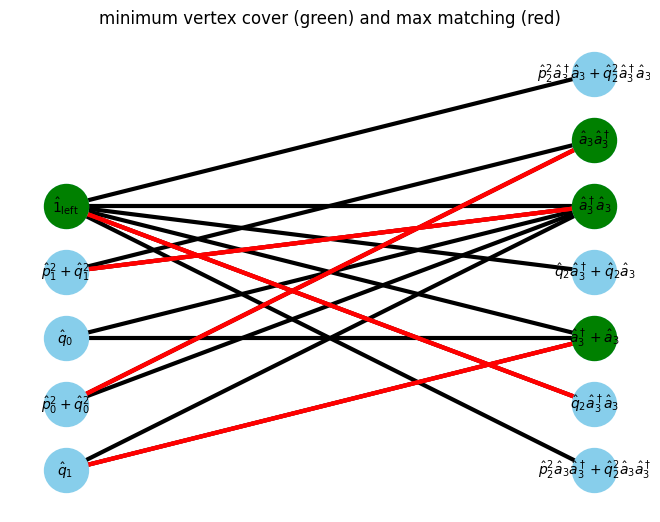
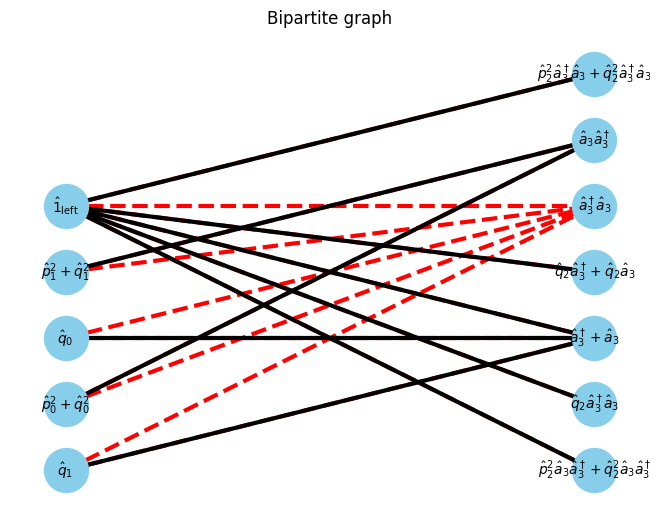
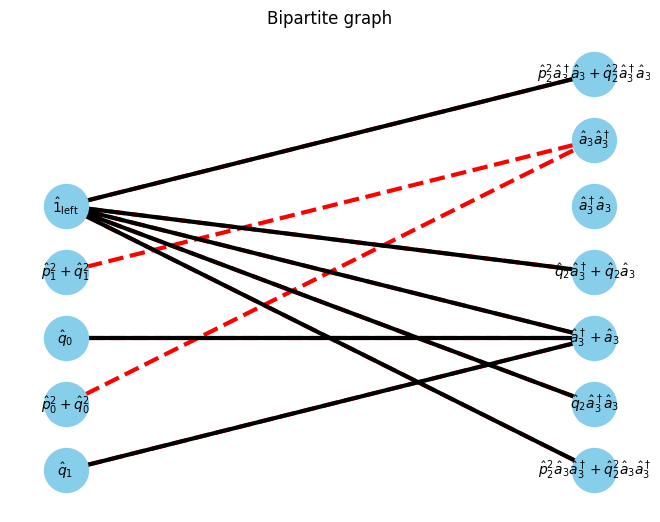
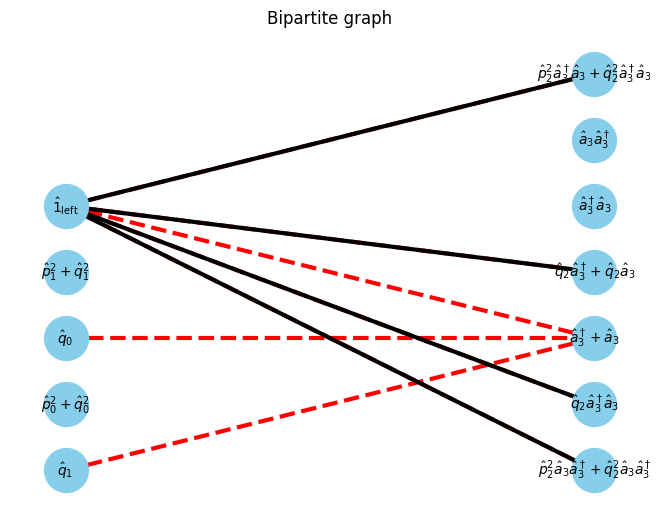
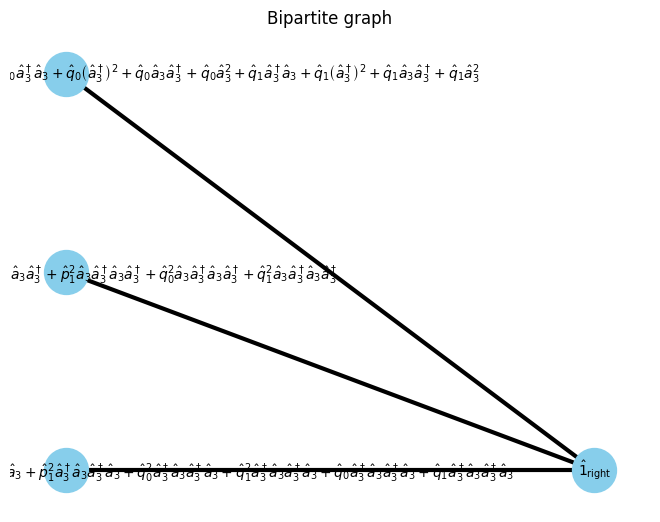
G, pos = show_bipartite(U, V, E)
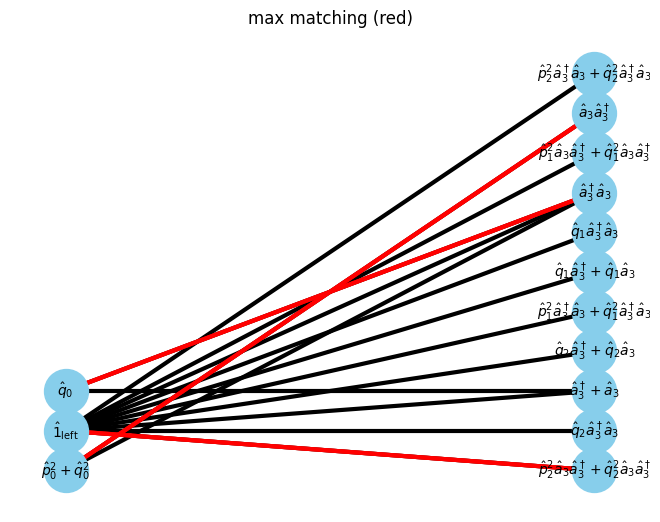
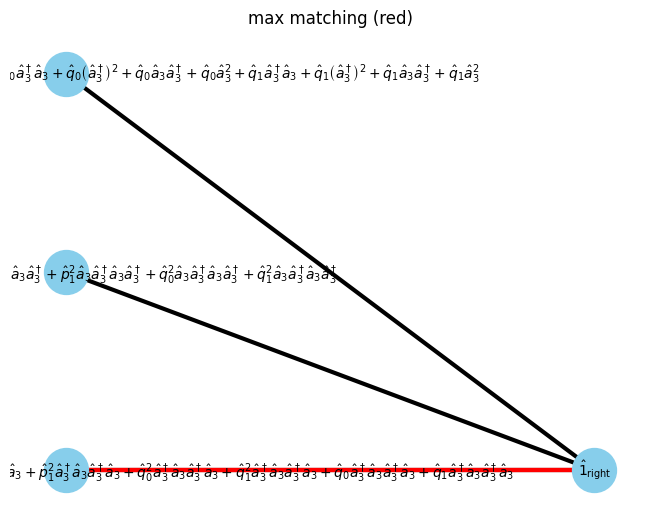
max_matching = show_maximal_matching(G, pos)
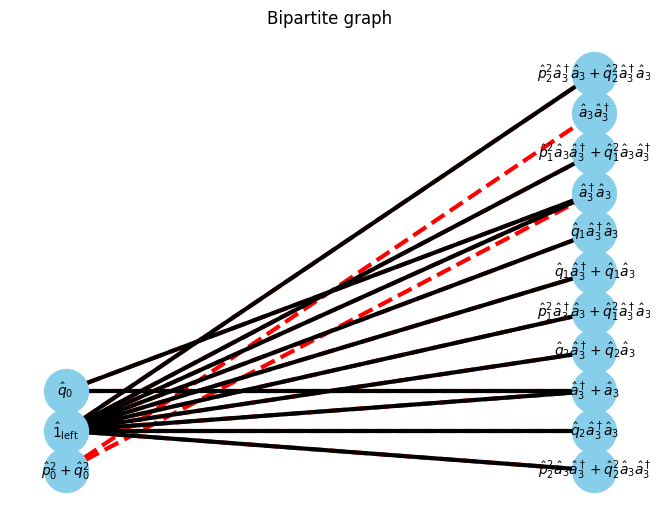
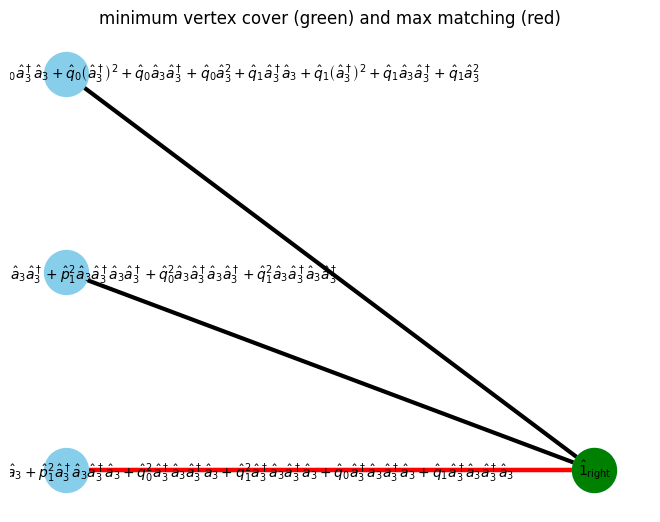
min_vertex_cover = show_min_vertex_cover(G, pos, max_matching)
Unew, Wi = assign_core(
min_vertex_cover=min_vertex_cover,
U=U,
V=V,
E=E,
operators=Hamiltonian,
isite=0,
W_assigns=W_assigns,
E_assigns=E_assigns,
coef_site=coef_site,
visualize=True,
)
W.append(Wi)
display(*W)
for isite in range(1, Hamiltonian.ndim):
print(f"{isite=}")
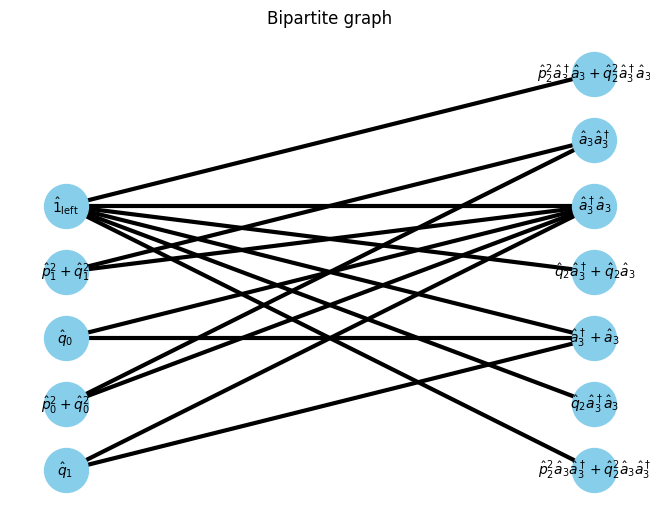
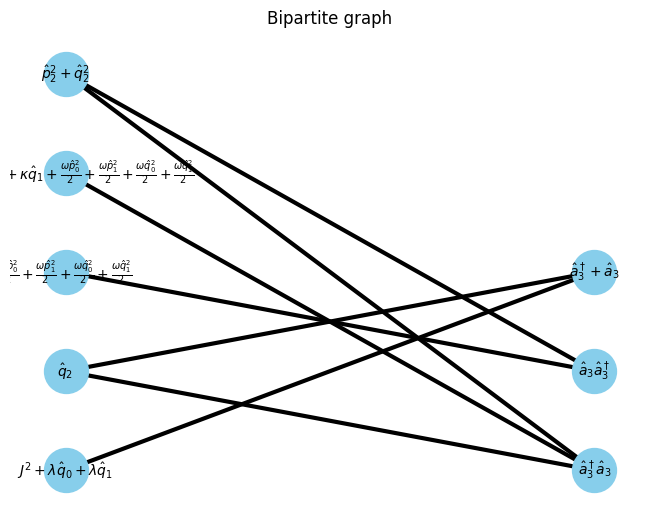
U, V, E, E_assigns = get_UVE(Hamiltonian, W_assigns, isite, Unew)
G, pos = show_bipartite(U, V, E)
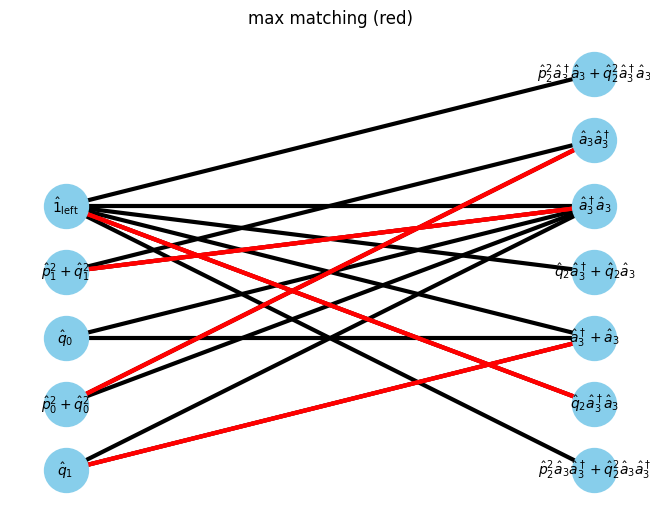
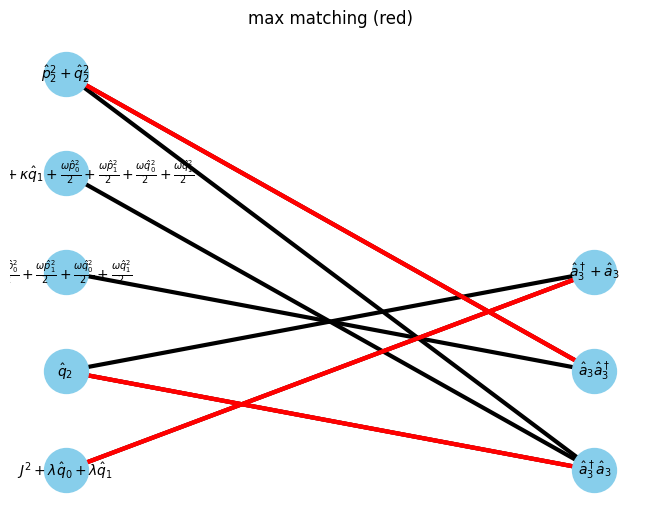
max_matching = show_maximal_matching(G, pos)
min_vertex_cover = show_min_vertex_cover(G, pos, max_matching)
Unew, Wi = assign_core(
min_vertex_cover=min_vertex_cover,
U=U,
V=V,
E=E,
operators=Hamiltonian,
isite=isite,
W_assigns=W_assigns,
E_assigns=E_assigns,
coef_site=coef_site,
visualize=True,
)
W.append(Wi)
display(*W)
W_prod = sympy.Mul(*W)
print(*[f"W{i}" for i in range(isite + 1)], "=")
display(W_prod.expand())

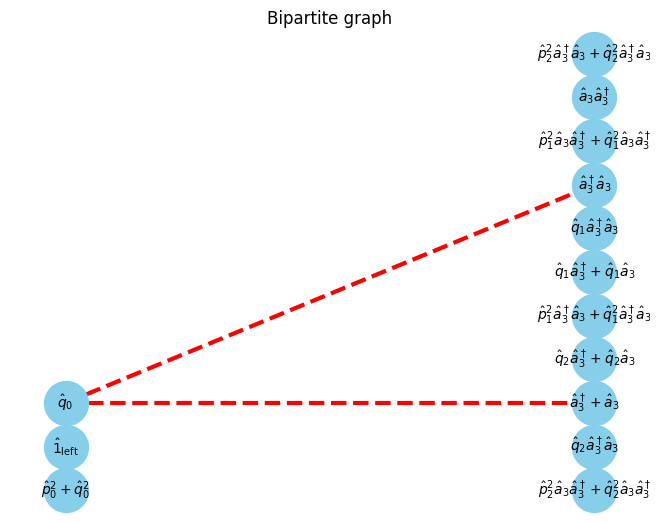
$\displaystyle \left[\begin{matrix}\hat{p}^2_0 + \hat{q}^2_0 & 1 & \hat{q}_0\end{matrix}\right]$
isite=1
$\displaystyle \left[\begin{matrix}\hat{p}^2_0 + \hat{q}^2_0 & 1 & \hat{q}_0\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}\frac{\omega}{2} & \frac{\omega}{2} & 0 & 0\\\Delta E + \kappa \hat{q}_1 + \frac{\omega \left(\hat{p}^2_1 + \hat{q}^2_1\right)}{2} & \frac{\omega \left(\hat{p}^2_1 + \hat{q}^2_1\right)}{2} & J + \lambda \hat{q}_1 & 1\\\kappa & 0 & \lambda & 0\end{matrix}\right]$
W0 W1 =
$\displaystyle \left[\begin{matrix}\Delta E + \kappa \hat{q}_0 + \kappa \hat{q}_1 + \frac{\omega \hat{p}^2_0}{2} + \frac{\omega \hat{p}^2_1}{2} + \frac{\omega \hat{q}^2_0}{2} + \frac{\omega \hat{q}^2_1}{2} & \frac{\omega \hat{p}^2_0}{2} + \frac{\omega \hat{p}^2_1}{2} + \frac{\omega \hat{q}^2_0}{2} + \frac{\omega \hat{q}^2_1}{2} & J + \lambda \hat{q}_0 + \lambda \hat{q}_1 & 1\end{matrix}\right]$
isite=2
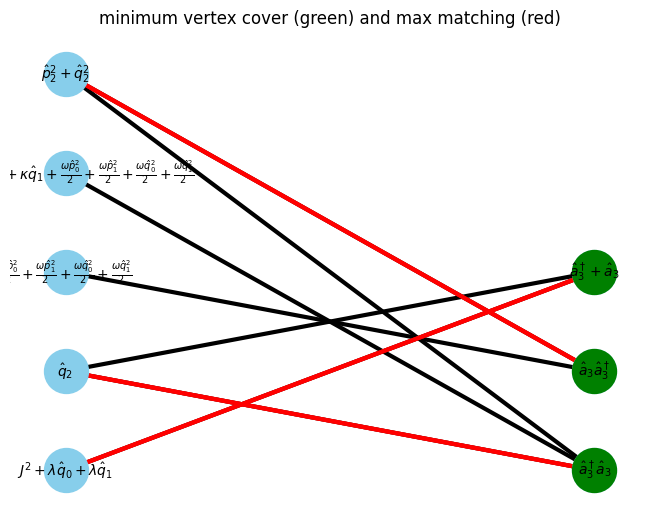
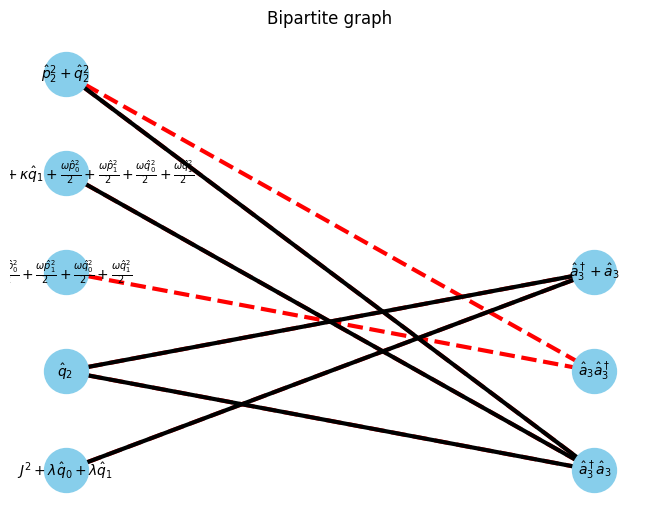
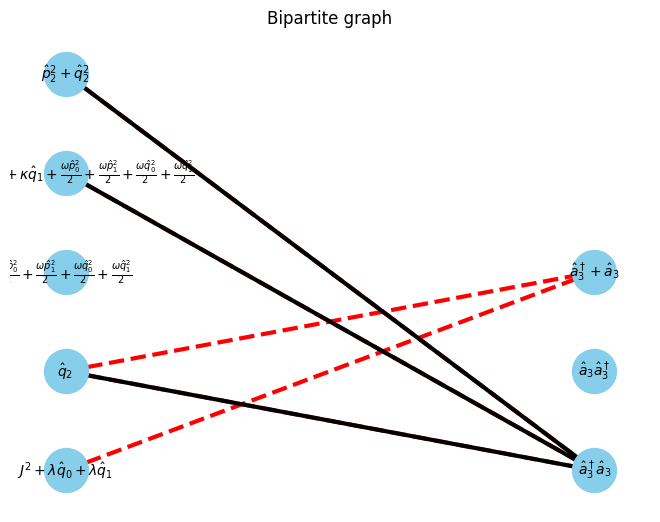
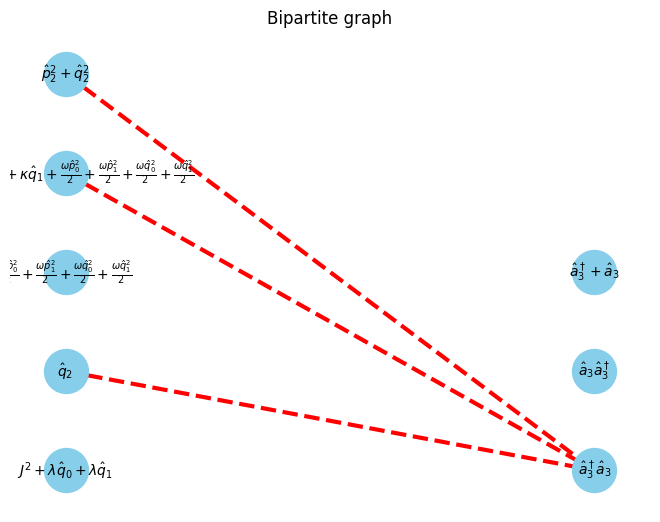
$\displaystyle \left[\begin{matrix}\hat{p}^2_0 + \hat{q}^2_0 & 1 & \hat{q}_0\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}\frac{\omega}{2} & \frac{\omega}{2} & 0 & 0\\\Delta E + \kappa \hat{q}_1 + \frac{\omega \left(\hat{p}^2_1 + \hat{q}^2_1\right)}{2} & \frac{\omega \left(\hat{p}^2_1 + \hat{q}^2_1\right)}{2} & J + \lambda \hat{q}_1 & 1\\\kappa & 0 & \lambda & 0\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 0 & 1\\1 & 0 & 0\\0 & 1 & 0\\\frac{\omega \left(\hat{p}^2_2 + \hat{q}^2_2\right)}{2} & \lambda \hat{q}_2 & \kappa \hat{q}_2 + \frac{\omega \left(\hat{p}^2_2 + \hat{q}^2_2\right)}{2}\end{matrix}\right]$
W0 W1 W2 =
$\displaystyle \left[\begin{matrix}\frac{\omega \hat{p}^2_0}{2} + \frac{\omega \hat{p}^2_1}{2} + \frac{\omega \hat{p}^2_2}{2} + \frac{\omega \hat{q}^2_0}{2} + \frac{\omega \hat{q}^2_1}{2} + \frac{\omega \hat{q}^2_2}{2} & J + \lambda \hat{q}_0 + \lambda \hat{q}_1 + \lambda \hat{q}_2 & \Delta E + \kappa \hat{q}_0 + \kappa \hat{q}_1 + \kappa \hat{q}_2 + \frac{\omega \hat{p}^2_0}{2} + \frac{\omega \hat{p}^2_1}{2} + \frac{\omega \hat{p}^2_2}{2} + \frac{\omega \hat{q}^2_0}{2} + \frac{\omega \hat{q}^2_1}{2} + \frac{\omega \hat{q}^2_2}{2}\end{matrix}\right]$
isite=3
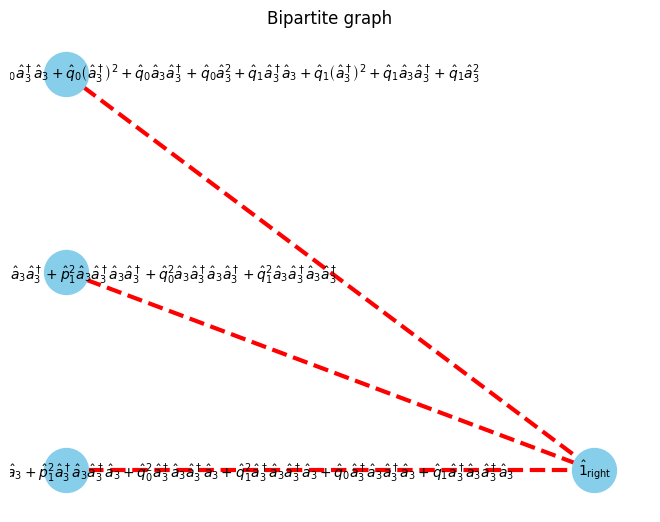
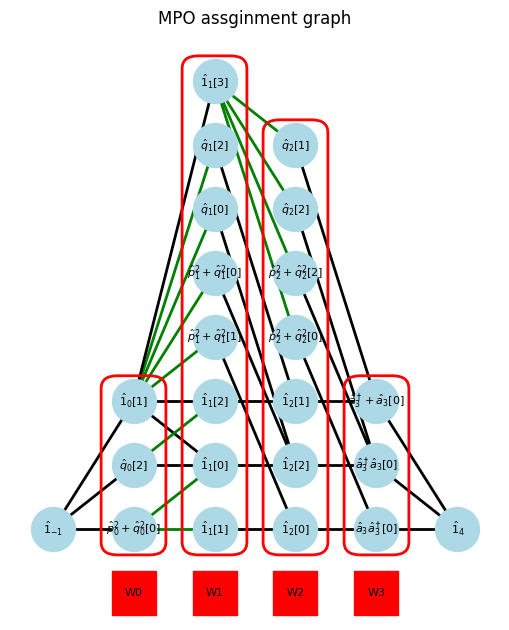
$\displaystyle \left[\begin{matrix}\hat{p}^2_0 + \hat{q}^2_0 & 1 & \hat{q}_0\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}\frac{\omega}{2} & \frac{\omega}{2} & 0 & 0\\\Delta E + \kappa \hat{q}_1 + \frac{\omega \left(\hat{p}^2_1 + \hat{q}^2_1\right)}{2} & \frac{\omega \left(\hat{p}^2_1 + \hat{q}^2_1\right)}{2} & J + \lambda \hat{q}_1 & 1\\\kappa & 0 & \lambda & 0\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 0 & 1\\1 & 0 & 0\\0 & 1 & 0\\\frac{\omega \left(\hat{p}^2_2 + \hat{q}^2_2\right)}{2} & \lambda \hat{q}_2 & \kappa \hat{q}_2 + \frac{\omega \left(\hat{p}^2_2 + \hat{q}^2_2\right)}{2}\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}\hat{a}_3 \hat{a}^\dagger_3\\\hat{a}^\dagger_3 + \hat{a}_3\\\hat{a}^\dagger_3 \hat{a}_3\end{matrix}\right]$
W0 W1 W2 W3 =
$\displaystyle \left[\begin{matrix}J \hat{a}^\dagger_3 + J \hat{a}_3 + \Delta E \hat{a}^\dagger_3 \hat{a}_3 + \kappa \hat{q}_0 \hat{a}^\dagger_3 \hat{a}_3 + \kappa \hat{q}_1 \hat{a}^\dagger_3 \hat{a}_3 + \kappa \hat{q}_2 \hat{a}^\dagger_3 \hat{a}_3 + \lambda \hat{q}_0 \hat{a}^\dagger_3 + \lambda \hat{q}_0 \hat{a}_3 + \lambda \hat{q}_1 \hat{a}^\dagger_3 + \lambda \hat{q}_1 \hat{a}_3 + \lambda \hat{q}_2 \hat{a}^\dagger_3 + \lambda \hat{q}_2 \hat{a}_3 + \frac{\omega \hat{p}^2_0 \hat{a}^\dagger_3 \hat{a}_3}{2} + \frac{\omega \hat{p}^2_0 \hat{a}_3 \hat{a}^\dagger_3}{2} + \frac{\omega \hat{p}^2_1 \hat{a}^\dagger_3 \hat{a}_3}{2} + \frac{\omega \hat{p}^2_1 \hat{a}_3 \hat{a}^\dagger_3}{2} + \frac{\omega \hat{p}^2_2 \hat{a}^\dagger_3 \hat{a}_3}{2} + \frac{\omega \hat{p}^2_2 \hat{a}_3 \hat{a}^\dagger_3}{2} + \frac{\omega \hat{q}^2_0 \hat{a}^\dagger_3 \hat{a}_3}{2} + \frac{\omega \hat{q}^2_0 \hat{a}_3 \hat{a}^\dagger_3}{2} + \frac{\omega \hat{q}^2_1 \hat{a}^\dagger_3 \hat{a}_3}{2} + \frac{\omega \hat{q}^2_1 \hat{a}_3 \hat{a}^\dagger_3}{2} + \frac{\omega \hat{q}^2_2 \hat{a}^\dagger_3 \hat{a}_3}{2} + \frac{\omega \hat{q}^2_2 \hat{a}_3 \hat{a}^\dagger_3}{2}\end{matrix}\right]$
Use AssignManager for whole assignment
[5]:
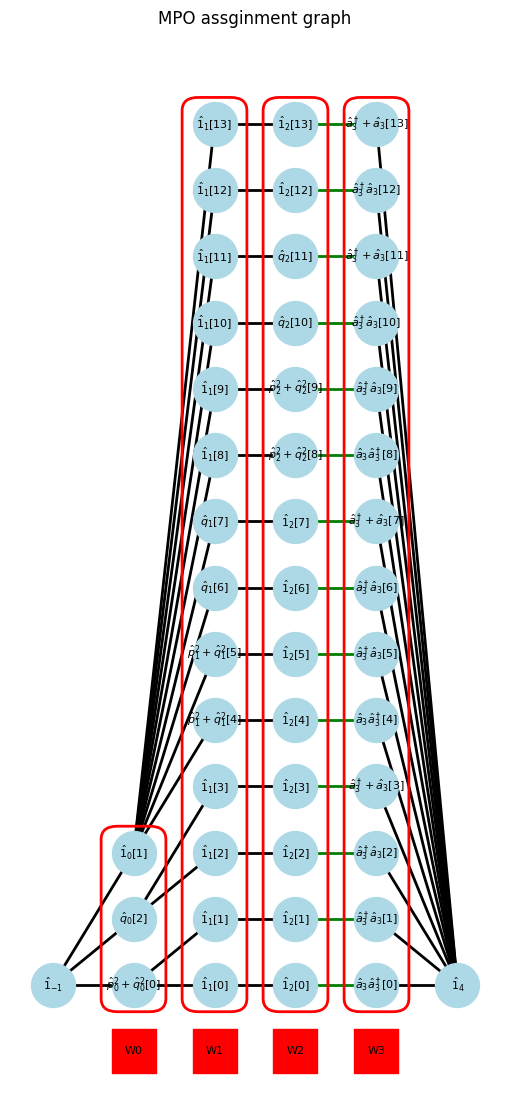
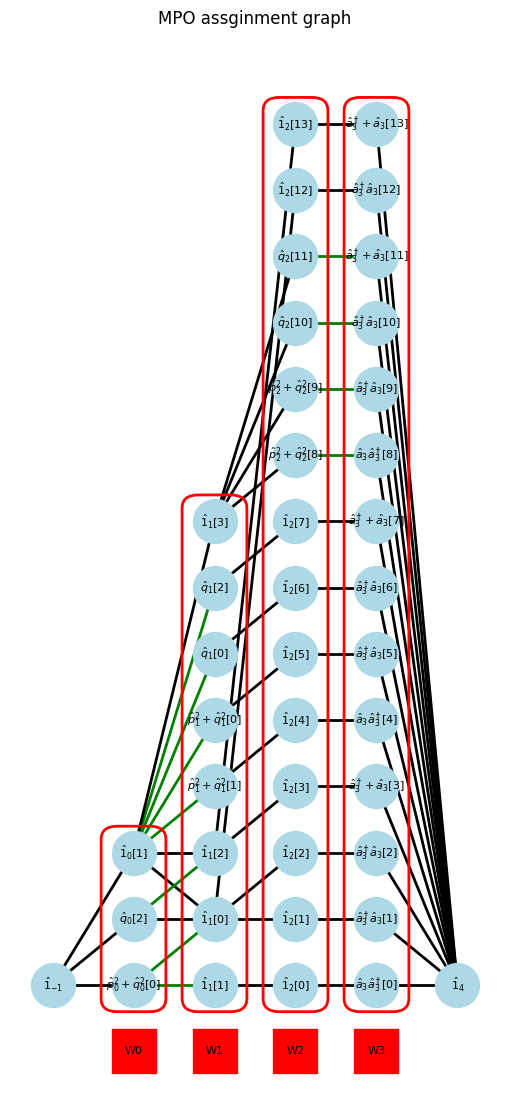
am = AssignManager(Holstein)
am.assign()
display(*am.Wsym)
2024-12-31 18:07:21.907 | INFO | pympo.bipartite:assign:286 - assigned 1/4
2024-12-31 18:07:21.908 | INFO | pympo.bipartite:assign:286 - assigned 2/4
2024-12-31 18:07:21.910 | INFO | pympo.bipartite:assign:286 - assigned 3/4
2024-12-31 18:07:21.911 | INFO | pympo.bipartite:assign:286 - assigned 4/4
$\displaystyle \left[\begin{matrix}\hat{p}^2_0 + \hat{q}^2_0 & 1 & \hat{q}_0\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & \frac{\omega}{2} & \frac{\omega}{2} & 0\\J + \lambda \hat{q}_1 & \frac{\omega \left(\hat{p}^2_1 + \hat{q}^2_1\right)}{2} & \Delta E + \kappa \hat{q}_1 + \frac{\omega \left(\hat{p}^2_1 + \hat{q}^2_1\right)}{2} & 1\\\lambda & 0 & \kappa & 0\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 0 & 1\\1 & 0 & 0\\0 & 1 & 0\\\frac{\omega \left(\hat{p}^2_2 + \hat{q}^2_2\right)}{2} & \kappa \hat{q}_2 + \frac{\omega \left(\hat{p}^2_2 + \hat{q}^2_2\right)}{2} & \lambda \hat{q}_2\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}\hat{a}_3 \hat{a}^\dagger_3\\\hat{a}^\dagger_3 \hat{a}_3\\\hat{a}^\dagger_3 + \hat{a}_3\end{matrix}\right]$
[6]:
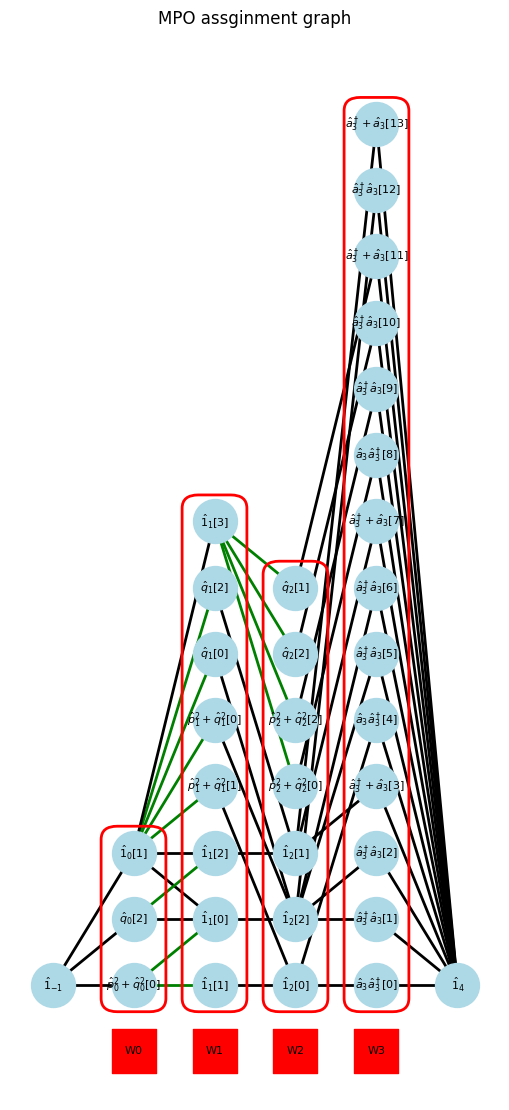
am.show_graph()
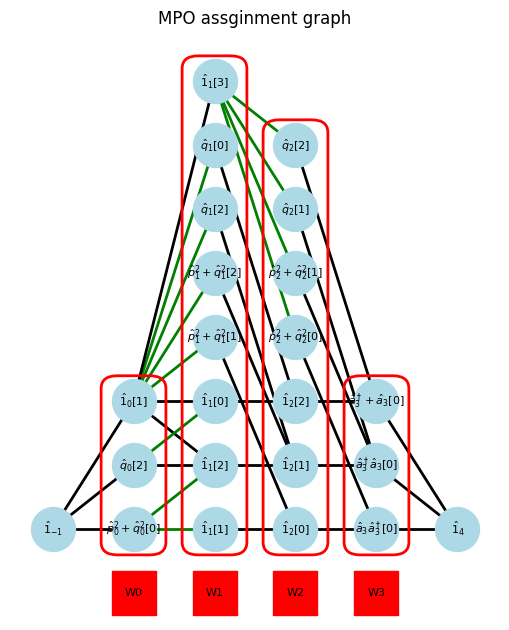
[7]:
W_prod = sympy.Mul(*am.Wsym)
print(*[f"W{i}" for i in range(am.ndim)], "=")
display(W_prod[0].expand())
W0 W1 W2 W3 =
$\displaystyle J \hat{a}^\dagger_3 + J \hat{a}_3 + \Delta E \hat{a}^\dagger_3 \hat{a}_3 + \kappa \hat{q}_0 \hat{a}^\dagger_3 \hat{a}_3 + \kappa \hat{q}_1 \hat{a}^\dagger_3 \hat{a}_3 + \kappa \hat{q}_2 \hat{a}^\dagger_3 \hat{a}_3 + \lambda \hat{q}_0 \hat{a}^\dagger_3 + \lambda \hat{q}_0 \hat{a}_3 + \lambda \hat{q}_1 \hat{a}^\dagger_3 + \lambda \hat{q}_1 \hat{a}_3 + \lambda \hat{q}_2 \hat{a}^\dagger_3 + \lambda \hat{q}_2 \hat{a}_3 + \frac{\omega \hat{p}^2_0 \hat{a}^\dagger_3 \hat{a}_3}{2} + \frac{\omega \hat{p}^2_0 \hat{a}_3 \hat{a}^\dagger_3}{2} + \frac{\omega \hat{p}^2_1 \hat{a}^\dagger_3 \hat{a}_3}{2} + \frac{\omega \hat{p}^2_1 \hat{a}_3 \hat{a}^\dagger_3}{2} + \frac{\omega \hat{p}^2_2 \hat{a}^\dagger_3 \hat{a}_3}{2} + \frac{\omega \hat{p}^2_2 \hat{a}_3 \hat{a}^\dagger_3}{2} + \frac{\omega \hat{q}^2_0 \hat{a}^\dagger_3 \hat{a}_3}{2} + \frac{\omega \hat{q}^2_0 \hat{a}_3 \hat{a}^\dagger_3}{2} + \frac{\omega \hat{q}^2_1 \hat{a}^\dagger_3 \hat{a}_3}{2} + \frac{\omega \hat{q}^2_1 \hat{a}_3 \hat{a}^\dagger_3}{2} + \frac{\omega \hat{q}^2_2 \hat{a}^\dagger_3 \hat{a}_3}{2} + \frac{\omega \hat{q}^2_2 \hat{a}_3 \hat{a}^\dagger_3}{2}$
[8]:
mpo = am.numerical_mpo(
subs={ΔE: 1.0, J: 1.0, lam: 1.0, omega: 1.0, kappa: 1.0}
) # subs is not necessary if you define its value in advance.
mpo
[8]:
[array([[[[2.+0.j, 1.+0.j, 1.+0.j],
[1.+0.j, 0.+0.j, 0.+0.j],
[1.+0.j, 0.+0.j, 0.+0.j]],
[[1.+0.j, 0.+0.j, 0.+0.j],
[2.+0.j, 1.+0.j, 1.+0.j],
[1.+0.j, 0.+0.j, 0.+0.j]],
[[1.+0.j, 0.+0.j, 0.+0.j],
[1.+0.j, 0.+0.j, 0.+0.j],
[2.+0.j, 1.+0.j, 1.+0.j]]]]),
array([[[[0. +0.j, 0.5+0.j, 0.5+0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j, 0. +0.j]],
[[0. +0.j, 0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0.5+0.j, 0.5+0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j, 0. +0.j]],
[[0. +0.j, 0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0.5+0.j, 0.5+0.j, 0. +0.j]]],
[[[2. +0.j, 1. +0.j, 3. +0.j, 1. +0.j],
[0. +0.j, 0.5+0.j, 0.5+0.j, 0. +0.j],
[0. +0.j, 0.5+0.j, 0.5+0.j, 0. +0.j]],
[[0. +0.j, 0.5+0.j, 0.5+0.j, 0. +0.j],
[2. +0.j, 1. +0.j, 3. +0.j, 1. +0.j],
[0. +0.j, 0.5+0.j, 0.5+0.j, 0. +0.j]],
[[0. +0.j, 0.5+0.j, 0.5+0.j, 0. +0.j],
[0. +0.j, 0.5+0.j, 0.5+0.j, 0. +0.j],
[2. +0.j, 1. +0.j, 3. +0.j, 1. +0.j]]],
[[[1. +0.j, 0. +0.j, 1. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j, 0. +0.j]],
[[0. +0.j, 0. +0.j, 0. +0.j, 0. +0.j],
[1. +0.j, 0. +0.j, 1. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j, 0. +0.j]],
[[0. +0.j, 0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j, 0. +0.j],
[1. +0.j, 0. +0.j, 1. +0.j, 0. +0.j]]]]),
array([[[[0. +0.j, 0. +0.j, 1. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j]],
[[0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 1. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j]],
[[0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 1. +0.j]]],
[[[1. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j]],
[[0. +0.j, 0. +0.j, 0. +0.j],
[1. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j]],
[[0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j],
[1. +0.j, 0. +0.j, 0. +0.j]]],
[[[0. +0.j, 1. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j]],
[[0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 1. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j]],
[[0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 1. +0.j, 0. +0.j]]],
[[[1. +0.j, 2. +0.j, 1. +0.j],
[0.5+0.j, 0.5+0.j, 0. +0.j],
[0.5+0.j, 0.5+0.j, 0. +0.j]],
[[0.5+0.j, 0.5+0.j, 0. +0.j],
[1. +0.j, 2. +0.j, 1. +0.j],
[0.5+0.j, 0.5+0.j, 0. +0.j]],
[[0.5+0.j, 0.5+0.j, 0. +0.j],
[0.5+0.j, 0.5+0.j, 0. +0.j],
[1. +0.j, 2. +0.j, 1. +0.j]]]]),
array([[[[0.+0.j],
[0.+0.j]],
[[0.+0.j],
[1.+0.j]]],
[[[1.+0.j],
[0.+0.j]],
[[0.+0.j],
[0.+0.j]]],
[[[0.+0.j],
[1.+0.j]],
[[1.+0.j],
[0.+0.j]]]])]