Execute Quantum Dynamics with PyTDSCF –Taylor expansion PES

[1]:

try:
    import pytdscf
except ModuleNotFoundError:
    !uv pip install -U git+https://github.com/QCLovers/PyTDSCF --quiet
try:
    import discvar
except ModuleNotFoundError:
    !uv pip install -U git+https://github.com/QCLovers/Discvar --quiet

[2]:

import itertools
from collections import defaultdict
from math import factorial, sqrt

import numpy as np
import sympy
from discvar import HarmonicOscillator as HO
from pytdscf import BasInfo, Model, Simulator, units
from pytdscf.dvr_operator_cls import TensorOperator
from pytdscf.hamiltonian_cls import TensorHamiltonian
from pytdscf.potentials.ch2o_potential import k_orig

import pympo

[3]:

backend = "jax"
m = 30
N = 9
Δt = 0.1
cutoff = 0.0  # 1.e-09

\[V - V_0 = \frac{k_{11}}{2!} Q_1^2 + \frac{k_{22}}{2!} Q_2^2 + \frac{k_{33}}{2!} Q_3^2 + \frac{k_{111}}{3!} Q_1^3 + \frac{k_{122}}{2!} Q_1Q_2^2 + \cdots\]

[4]:

print(f"{len(k_orig)=}")
active_modes = sorted(list(set(itertools.chain.from_iterable(k_orig.keys()))))
index = {}
for i, mode in enumerate(active_modes):
    index[mode] = i
print(f"{index=}")
f = len(active_modes)
k_new = {}
for key, value in k_orig.items():
    new_key = tuple([index[k] for k in key])
    if abs(value) > cutoff:
        k_new[new_key] = value
print(f"{len(k_new)=}")

len(k_orig)=114
index={1: 0, 2: 1, 3: 2, 4: 3, 5: 4, 6: 5}
len(k_new)=114

[5]:

k_new

[5]:

{(0, 0): 2.881141028397287e-05,
 (1, 1): 3.2448494255464496e-05,
 (2, 2): 4.725466264016419e-05,
 (3, 3): 6.805132227202656e-05,
 (4, 4): 0.00017348287106252062,
 (5, 5): 0.0001808886981537931,
 (2, 2, 2): -1.1756574314828089e-07,
 (3, 3, 3): 1.956730822300732e-06,
 (4, 4, 4): 9.330094468538158e-06,
 (5, 5, 5): -9.893510625593033e-09,
 (0, 0, 2): -1.238616135463855e-07,
 (1, 1, 2): 2.3333266618281752e-07,
 (0, 3, 3): 7.709229058903663e-10,
 (0, 0, 3): 6.899760007718777e-08,
 (1, 1, 3): 4.7154784410294076e-08,
 (2, 3, 3): 3.410048987055054e-07,
 (2, 2, 3): 2.858839109343442e-07,
 (0, 4, 4): 2.955204472579738e-09,
 (0, 0, 4): -9.109739004604497e-07,
 (1, 1, 4): -6.881771806581336e-07,
 (2, 4, 4): -7.439406041842036e-08,
 (2, 2, 4): -3.3560843836427284e-07,
 (3, 4, 4): -9.31531844617526e-08,
 (3, 3, 4): -2.9128037127557674e-07,
 (0, 5, 5): 3.2121787745431932e-09,
 (2, 5, 5): 6.435921392674742e-07,
 (3, 5, 5): -6.933166666974028e-07,
 (4, 5, 5): 1.0040242952014167e-05,
 (4, 4, 5): 3.4691530765066486e-09,
 (0, 1, 4): -5.13948603926911e-10,
 (0, 3, 4): -6.424357549086387e-10,
 (2, 3, 4): 2.4720927848884413e-07,
 (0, 1, 5): -1.798820113744188e-09,
 (0, 2, 5): 1.027897207853822e-09,
 (1, 2, 5): 6.678762108030208e-07,
 (0, 3, 5): -6.424357549086386e-10,
 (1, 3, 5): -4.840110977481683e-07,
 (1, 4, 5): -2.980901902776083e-08,
 (0, 0, 0, 0): 1.7939020286070263e-08,
 (1, 1, 1, 1): 1.4535391374218987e-08,
 (2, 2, 2, 2): 5.3808032664810655e-09,
 (3, 3, 3, 3): 5.192114024418222e-08,
 (4, 4, 4, 4): 4.229558138073721e-07,
 (5, 5, 5, 5): 5.069812097824381e-07,
 (0, 1, 1, 1): 8.727253620131479e-11,
 (0, 0, 1, 1): 4.207138124463382e-09,
 (0, 0, 0, 1): 1.5046989000226694e-10,
 (0, 0, 2, 2): 2.2841329302344115e-09,
 (1, 1, 2, 2): 8.314966121525269e-09,
 (0, 3, 3, 3): 2.4075182400362706e-11,
 (0, 0, 3, 3): -2.317236306034911e-09,
 (1, 1, 3, 3): -9.028193400136016e-11,
 (2, 3, 3, 3): 9.928003342349572e-09,
 (2, 2, 3, 3): 4.613406827469504e-09,
 (2, 2, 2, 3): -3.2351026350487387e-09,
 (0, 4, 4, 4): 1.594980834024029e-10,
 (0, 0, 4, 4): -8.878024449913753e-08,
 (0, 0, 0, 4): -7.222554720108814e-11,
 (1, 4, 4, 4): -2.7084580200408045e-11,
 (1, 1, 4, 4): -7.305012219830055e-08,
 (2, 4, 4, 4): -4.9173560052740825e-09,
 (2, 2, 4, 4): -6.238180699713982e-08,
 (2, 2, 2, 4): -5.537291952083423e-09,
 (3, 4, 4, 4): -6.918605542304234e-09,
 (3, 3, 4, 4): -1.3683731796806156e-08,
 (3, 3, 3, 4): -4.526134291268189e-09,
 (0, 5, 5, 5): -3.9122171400589393e-10,
 (0, 0, 5, 5): -1.0699612938281198e-07,
 (0, 0, 0, 5): -8.727253620131484e-11,
 (1, 5, 5, 5): -3.2606825163491245e-08,
 (1, 1, 5, 5): -7.859042354818399e-08,
 (1, 1, 1, 5): -4.568265860468825e-09,
 (2, 2, 5, 5): -8.568357416289087e-08,
 (3, 3, 5, 5): -2.4649977380171364e-08,
 (4, 5, 5, 5): -2.828833932042618e-10,
 (4, 4, 5, 5): 4.6045591979373705e-07,
 (4, 4, 4, 5): 3.220055646048512e-10,
 (0, 1, 2, 2): 9.329133180140548e-11,
 (0, 1, 1, 2): -2.1065784600317367e-11,
 (0, 1, 3, 3): 2.4075182400362706e-11,
 (0, 1, 1, 3): 1.2037591200181356e-11,
 (0, 0, 2, 3): -2.287142328034457e-09,
 (1, 1, 2, 3): -4.083752814661525e-09,
 (0, 1, 4, 4): -8.426313840126947e-11,
 (0, 1, 1, 4): -2.7084580200408045e-11,
 (0, 2, 4, 4): -1.2037591200181355e-11,
 (0, 2, 2, 4): -2.1065784600317367e-11,
 (0, 0, 2, 4): -2.949209844044432e-09,
 (1, 2, 4, 4): 4.514096700068007e-11,
 (1, 1, 2, 4): 6.503308645897975e-09,
 (0, 3, 4, 4): -1.8056386800272028e-11,
 (0, 0, 3, 4): 5.29954952587984e-09,
 (1, 3, 4, 4): -2.1065784600317367e-11,
 (1, 1, 3, 4): 3.737672067656311e-09,
 (2, 3, 4, 4): 3.1707015221277685e-08,
 (2, 3, 3, 4): -5.359737481880746e-09,
 (2, 2, 3, 4): 7.472334737512576e-09,
 (0, 1, 5, 5): -1.0833832080163219e-10,
 (0, 0, 1, 5): 3.731653272056219e-10,
 (0, 2, 5, 5): -1.2037591200181355e-11,
 (1, 2, 5, 5): -4.8150364800725425e-11,
 (1, 2, 2, 5): 5.109957464476984e-09,
 (0, 3, 5, 5): -2.4075182400362706e-11,
 (1, 3, 5, 5): 2.407518240036271e-11,
 (1, 3, 3, 5): 2.6001196992391727e-09,
 (2, 3, 5, 5): 4.3199905419650836e-08,
 (0, 4, 5, 5): 1.4746049220222154e-10,
 (0, 4, 4, 5): -3.340431558050326e-10,
 (1, 4, 5, 5): -3.611277360054406e-11,
 (1, 4, 4, 5): 2.0463905040308303e-10,
 (2, 4, 5, 5): 2.8249217149025584e-08,
 (2, 4, 4, 5): 4.815036480072542e-11,
 (3, 4, 5, 5): -2.4045088422362252e-08,
 (3, 4, 4, 5): -2.7084580200408048e-11}

[6]:

freqs = [
    sqrt(k_new[(k, k)]) * units.au_in_cm1 for k in range(f)
]  # a.u. (sqrt{omega^2} = omega)
freqs  # in cm^{-1}

[6]:

[1178.0577664330528,
 1250.20606814231,
 1508.7131015744023,
 1810.5170221732483,
 2890.763940664299,
 2951.821181690477]

[7]:

nprims = [N] * f  # Number of primitive basis
dvr_prims = [
    # HO(ngrid=nprim, omega=omega, units='cm-1')
    HO(nprim, omega)
    for nprim, omega in zip(nprims, freqs, strict=True)
]
dvr_prims_redundant = [
    # HO(ngrid=nprim, omega=omega, units='cm-1')
    HO(nprim+4, omega)
    for nprim, omega in zip(nprims, freqs, strict=True)
]
ndof = len(dvr_prims)  # Number of degree of freedom
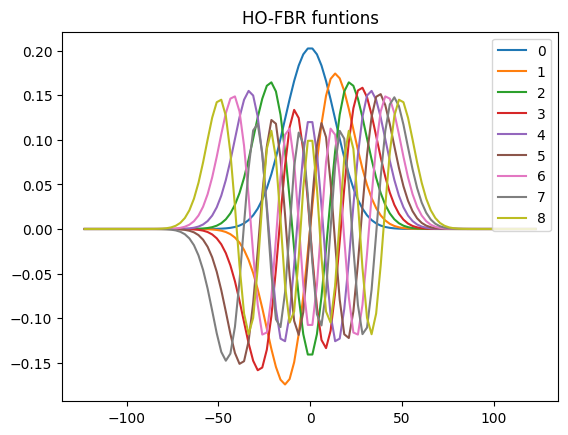
basinfo = BasInfo([dvr_prims], spf_info=None)  # Set basis information object

dvr_prims[0].plot_fbr()

../_images/example_pytdscf-taylor_8_0.png

[8]:

dq2 = [prim.get_2nd_derivative_matrix_fbr() for prim in dvr_prims]
q_scale = 10
q1 = [prim.get_pos_rep_matrix() / q_scale for prim in dvr_prims_redundant]
q2 = [ints @ ints for ints in q1]
q3 = [ints @ ints @ ints for ints in q1]
q4 = [ints @ ints @ ints @ ints for ints in q1]
qn = [[ints[:N, :N] for ints in q] for q in [q1, q2, q3, q4]]

[9]:

kinetic_sop = pympo.SumOfProducts([])
for isite in range(f):
    kinetic_sop -= (
        1
        / 2
        * pympo.OpSite(
            r"\frac{\partial}{\partial q^2_{" + f"{isite}" + r"}}",
            isite,
            value=dq2[isite],
        )
    )
kinetic_sop.symbol

[9]:

$\displaystyle - 0.5 \frac{\partial}{\partial q^2_{0}} - 0.5 \frac{\partial}{\partial q^2_{1}} - 0.5 \frac{\partial}{\partial q^2_{2}} - 0.5 \frac{\partial}{\partial q^2_{3}} - 0.5 \frac{\partial}{\partial q^2_{4}} - 0.5 \frac{\partial}{\partial q^2_{5}}$

[10]:

potential_sop = pympo.SumOfProducts([])
coef_symbol = {}
for key, coef in k_new.items():
    cnt_site = defaultdict(int)
    for isite in key:
        cnt_site[isite] += 1
    op = 1
    coef_sym = sympy.Symbol(f"k_{key}")
    for isite, order in cnt_site.items():
        coef /= factorial(order)
        op *= pympo.OpSite(
            f"q^{order}" + r"_{" + f"{isite}" + r"}",
            isite,
            value=qn[order - 1][isite],
        )
    op *= coef_sym
    coef_symbol[coef_sym] = coef * (q_scale ** len(key))
    potential_sop += op
potential_sop.symbol

[10]:

$\displaystyle k_{(0, 0)} q^2_{0} + k_{(0, 0, 0, 0)} q^4_{0} + k_{(0, 0, 0, 1)} q^3_{0} q^1_{1} + k_{(0, 0, 0, 4)} q^3_{0} q^1_{4} + k_{(0, 0, 0, 5)} q^3_{0} q^1_{5} + k_{(0, 0, 1, 1)} q^2_{0} q^2_{1} + k_{(0, 0, 1, 5)} q^2_{0} q^1_{1} q^1_{5} + k_{(0, 0, 2)} q^2_{0} q^1_{2} + k_{(0, 0, 2, 2)} q^2_{0} q^2_{2} + k_{(0, 0, 2, 3)} q^2_{0} q^1_{2} q^1_{3} + k_{(0, 0, 2, 4)} q^2_{0} q^1_{2} q^1_{4} + k_{(0, 0, 3)} q^2_{0} q^1_{3} + k_{(0, 0, 3, 3)} q^2_{0} q^2_{3} + k_{(0, 0, 3, 4)} q^2_{0} q^1_{3} q^1_{4} + k_{(0, 0, 4)} q^2_{0} q^1_{4} + k_{(0, 0, 4, 4)} q^2_{0} q^2_{4} + k_{(0, 0, 5, 5)} q^2_{0} q^2_{5} + k_{(0, 1, 1, 1)} q^1_{0} q^3_{1} + k_{(0, 1, 1, 2)} q^1_{0} q^2_{1} q^1_{2} + k_{(0, 1, 1, 3)} q^1_{0} q^2_{1} q^1_{3} + k_{(0, 1, 1, 4)} q^1_{0} q^2_{1} q^1_{4} + k_{(0, 1, 2, 2)} q^1_{0} q^1_{1} q^2_{2} + k_{(0, 1, 3, 3)} q^1_{0} q^1_{1} q^2_{3} + k_{(0, 1, 4)} q^1_{0} q^1_{1} q^1_{4} + k_{(0, 1, 4, 4)} q^1_{0} q^1_{1} q^2_{4} + k_{(0, 1, 5)} q^1_{0} q^1_{1} q^1_{5} + k_{(0, 1, 5, 5)} q^1_{0} q^1_{1} q^2_{5} + k_{(0, 2, 2, 4)} q^1_{0} q^2_{2} q^1_{4} + k_{(0, 2, 4, 4)} q^1_{0} q^1_{2} q^2_{4} + k_{(0, 2, 5)} q^1_{0} q^1_{2} q^1_{5} + k_{(0, 2, 5, 5)} q^1_{0} q^1_{2} q^2_{5} + k_{(0, 3, 3)} q^1_{0} q^2_{3} + k_{(0, 3, 3, 3)} q^1_{0} q^3_{3} + k_{(0, 3, 4)} q^1_{0} q^1_{3} q^1_{4} + k_{(0, 3, 4, 4)} q^1_{0} q^1_{3} q^2_{4} + k_{(0, 3, 5)} q^1_{0} q^1_{3} q^1_{5} + k_{(0, 3, 5, 5)} q^1_{0} q^1_{3} q^2_{5} + k_{(0, 4, 4)} q^1_{0} q^2_{4} + k_{(0, 4, 4, 4)} q^1_{0} q^3_{4} + k_{(0, 4, 4, 5)} q^1_{0} q^2_{4} q^1_{5} + k_{(0, 4, 5, 5)} q^1_{0} q^1_{4} q^2_{5} + k_{(0, 5, 5)} q^1_{0} q^2_{5} + k_{(0, 5, 5, 5)} q^1_{0} q^3_{5} + k_{(1, 1)} q^2_{1} + k_{(1, 1, 1, 1)} q^4_{1} + k_{(1, 1, 1, 5)} q^3_{1} q^1_{5} + k_{(1, 1, 2)} q^2_{1} q^1_{2} + k_{(1, 1, 2, 2)} q^2_{1} q^2_{2} + k_{(1, 1, 2, 3)} q^2_{1} q^1_{2} q^1_{3} + k_{(1, 1, 2, 4)} q^2_{1} q^1_{2} q^1_{4} + k_{(1, 1, 3)} q^2_{1} q^1_{3} + k_{(1, 1, 3, 3)} q^2_{1} q^2_{3} + k_{(1, 1, 3, 4)} q^2_{1} q^1_{3} q^1_{4} + k_{(1, 1, 4)} q^2_{1} q^1_{4} + k_{(1, 1, 4, 4)} q^2_{1} q^2_{4} + k_{(1, 1, 5, 5)} q^2_{1} q^2_{5} + k_{(1, 2, 2, 5)} q^1_{1} q^2_{2} q^1_{5} + k_{(1, 2, 4, 4)} q^1_{1} q^1_{2} q^2_{4} + k_{(1, 2, 5)} q^1_{1} q^1_{2} q^1_{5} + k_{(1, 2, 5, 5)} q^1_{1} q^1_{2} q^2_{5} + k_{(1, 3, 3, 5)} q^1_{1} q^2_{3} q^1_{5} + k_{(1, 3, 4, 4)} q^1_{1} q^1_{3} q^2_{4} + k_{(1, 3, 5)} q^1_{1} q^1_{3} q^1_{5} + k_{(1, 3, 5, 5)} q^1_{1} q^1_{3} q^2_{5} + k_{(1, 4, 4, 4)} q^1_{1} q^3_{4} + k_{(1, 4, 4, 5)} q^1_{1} q^2_{4} q^1_{5} + k_{(1, 4, 5)} q^1_{1} q^1_{4} q^1_{5} + k_{(1, 4, 5, 5)} q^1_{1} q^1_{4} q^2_{5} + k_{(1, 5, 5, 5)} q^1_{1} q^3_{5} + k_{(2, 2)} q^2_{2} + k_{(2, 2, 2)} q^3_{2} + k_{(2, 2, 2, 2)} q^4_{2} + k_{(2, 2, 2, 3)} q^3_{2} q^1_{3} + k_{(2, 2, 2, 4)} q^3_{2} q^1_{4} + k_{(2, 2, 3)} q^2_{2} q^1_{3} + k_{(2, 2, 3, 3)} q^2_{2} q^2_{3} + k_{(2, 2, 3, 4)} q^2_{2} q^1_{3} q^1_{4} + k_{(2, 2, 4)} q^2_{2} q^1_{4} + k_{(2, 2, 4, 4)} q^2_{2} q^2_{4} + k_{(2, 2, 5, 5)} q^2_{2} q^2_{5} + k_{(2, 3, 3)} q^1_{2} q^2_{3} + k_{(2, 3, 3, 3)} q^1_{2} q^3_{3} + k_{(2, 3, 3, 4)} q^1_{2} q^2_{3} q^1_{4} + k_{(2, 3, 4)} q^1_{2} q^1_{3} q^1_{4} + k_{(2, 3, 4, 4)} q^1_{2} q^1_{3} q^2_{4} + k_{(2, 3, 5, 5)} q^1_{2} q^1_{3} q^2_{5} + k_{(2, 4, 4)} q^1_{2} q^2_{4} + k_{(2, 4, 4, 4)} q^1_{2} q^3_{4} + k_{(2, 4, 4, 5)} q^1_{2} q^2_{4} q^1_{5} + k_{(2, 4, 5, 5)} q^1_{2} q^1_{4} q^2_{5} + k_{(2, 5, 5)} q^1_{2} q^2_{5} + k_{(3, 3)} q^2_{3} + k_{(3, 3, 3)} q^3_{3} + k_{(3, 3, 3, 3)} q^4_{3} + k_{(3, 3, 3, 4)} q^3_{3} q^1_{4} + k_{(3, 3, 4)} q^2_{3} q^1_{4} + k_{(3, 3, 4, 4)} q^2_{3} q^2_{4} + k_{(3, 3, 5, 5)} q^2_{3} q^2_{5} + k_{(3, 4, 4)} q^1_{3} q^2_{4} + k_{(3, 4, 4, 4)} q^1_{3} q^3_{4} + k_{(3, 4, 4, 5)} q^1_{3} q^2_{4} q^1_{5} + k_{(3, 4, 5, 5)} q^1_{3} q^1_{4} q^2_{5} + k_{(3, 5, 5)} q^1_{3} q^2_{5} + k_{(4, 4)} q^2_{4} + k_{(4, 4, 4)} q^3_{4} + k_{(4, 4, 4, 4)} q^4_{4} + k_{(4, 4, 4, 5)} q^3_{4} q^1_{5} + k_{(4, 4, 5)} q^2_{4} q^1_{5} + k_{(4, 4, 5, 5)} q^2_{4} q^2_{5} + k_{(4, 5, 5)} q^1_{4} q^2_{5} + k_{(4, 5, 5, 5)} q^1_{4} q^3_{5} + k_{(5, 5)} q^2_{5} + k_{(5, 5, 5)} q^3_{5} + k_{(5, 5, 5, 5)} q^4_{5}$

[11]:

coef_symbol

[11]:

{k_(0, 0): 0.0014405705141986437,
 k_(1, 1): 0.001622424712773225,
 k_(2, 2): 0.002362733132008209,
 k_(3, 3): 0.003402566113601328,
 k_(4, 4): 0.008674143553126032,
 k_(5, 5): 0.009044434907689655,
 k_(2, 2, 2): -1.959429052471348e-05,
 k_(3, 3, 3): 0.00032612180371678867,
 k_(4, 4, 4): 0.0015550157447563595,
 k_(5, 5, 5): -1.6489184375988388e-06,
 k_(0, 0, 2): -6.193080677319275e-05,
 k_(1, 1, 2): 0.00011666633309140877,
 k_(0, 3, 3): 3.8546145294518314e-07,
 k_(0, 0, 3): 3.4498800038593886e-05,
 k_(1, 1, 3): 2.3577392205147037e-05,
 k_(2, 3, 3): 0.0001705024493527527,
 k_(2, 2, 3): 0.0001429419554671721,
 k_(0, 4, 4): 1.477602236289869e-06,
 k_(0, 0, 4): -0.00045548695023022486,
 k_(1, 1, 4): -0.0003440885903290668,
 k_(2, 4, 4): -3.719703020921018e-05,
 k_(2, 2, 4): -0.0001678042191821364,
 k_(3, 4, 4): -4.65765922308763e-05,
 k_(3, 3, 4): -0.00014564018563778837,
 k_(0, 5, 5): 1.6060893872715966e-06,
 k_(2, 5, 5): 0.0003217960696337371,
 k_(3, 5, 5): -0.0003466583333487014,
 k_(4, 5, 5): 0.005020121476007083,
 k_(4, 4, 5): 1.7345765382533244e-06,
 k_(0, 1, 4): -5.13948603926911e-07,
 k_(0, 3, 4): -6.424357549086388e-07,
 k_(2, 3, 4): 0.00024720927848884415,
 k_(0, 1, 5): -1.798820113744188e-06,
 k_(0, 2, 5): 1.027897207853822e-06,
 k_(1, 2, 5): 0.0006678762108030207,
 k_(0, 3, 5): -6.424357549086387e-07,
 k_(1, 3, 5): -0.0004840110977481683,
 k_(1, 4, 5): -2.980901902776083e-05,
 k_(0, 0, 0, 0): 7.47459178586261e-06,
 k_(1, 1, 1, 1): 6.056413072591244e-06,
 k_(2, 2, 2, 2): 2.242001361033777e-06,
 k_(3, 3, 3, 3): 2.1633808435075923e-05,
 k_(4, 4, 4, 4): 0.00017623158908640504,
 k_(5, 5, 5, 5): 0.00021124217074268252,
 k_(0, 1, 1, 1): 1.4545422700219133e-07,
 k_(0, 0, 1, 1): 1.0517845311158455e-05,
 k_(0, 0, 0, 1): 2.507831500037782e-07,
 k_(0, 0, 2, 2): 5.710332325586029e-06,
 k_(1, 1, 2, 2): 2.0787415303813172e-05,
 k_(0, 3, 3, 3): 4.0125304000604505e-08,
 k_(0, 0, 3, 3): -5.793090765087277e-06,
 k_(1, 1, 3, 3): -2.257048350034004e-07,
 k_(2, 3, 3, 3): 1.6546672237249285e-05,
 k_(2, 2, 3, 3): 1.1533517068673759e-05,
 k_(2, 2, 2, 3): -5.3918377250812315e-06,
 k_(0, 4, 4, 4): 2.6583013900400484e-07,
 k_(0, 0, 4, 4): -0.00022195061124784382,
 k_(0, 0, 0, 4): -1.2037591200181357e-07,
 k_(1, 4, 4, 4): -4.5140967000680075e-08,
 k_(1, 1, 4, 4): -0.00018262530549575137,
 k_(2, 4, 4, 4): -8.195593342123471e-06,
 k_(2, 2, 4, 4): -0.00015595451749284955,
 k_(2, 2, 2, 4): -9.228819920139039e-06,
 k_(3, 4, 4, 4): -1.1531009237173723e-05,
 k_(3, 3, 4, 4): -3.420932949201539e-05,
 k_(3, 3, 3, 4): -7.543557152113648e-06,
 k_(0, 5, 5, 5): -6.520361900098232e-07,
 k_(0, 0, 5, 5): -0.00026749032345702993,
 k_(0, 0, 0, 5): -1.454542270021914e-07,
 k_(1, 5, 5, 5): -5.434470860581874e-05,
 k_(1, 1, 5, 5): -0.00019647605887045997,
 k_(1, 1, 1, 5): -7.6137764341147074e-06,
 k_(2, 2, 5, 5): -0.00021420893540722717,
 k_(3, 3, 5, 5): -6.162494345042841e-05,
 k_(4, 5, 5, 5): -4.71472322007103e-07,
 k_(4, 4, 5, 5): 0.0011511397994843427,
 k_(4, 4, 4, 5): 5.366759410080853e-07,
 k_(0, 1, 2, 2): 4.6645665900702737e-07,
 k_(0, 1, 1, 2): -1.0532892300158684e-07,
 k_(0, 1, 3, 3): 1.2037591200181354e-07,
 k_(0, 1, 1, 3): 6.018795600090678e-08,
 k_(0, 0, 2, 3): -1.1435711640172285e-05,
 k_(1, 1, 2, 3): -2.0418764073307625e-05,
 k_(0, 1, 4, 4): -4.2131569200634735e-07,
 k_(0, 1, 1, 4): -1.3542290100204023e-07,
 k_(0, 2, 4, 4): -6.018795600090677e-08,
 k_(0, 2, 2, 4): -1.0532892300158684e-07,
 k_(0, 0, 2, 4): -1.4746049220222159e-05,
 k_(1, 2, 4, 4): 2.2570483500340037e-07,
 k_(1, 1, 2, 4): 3.251654322948988e-05,
 k_(0, 3, 4, 4): -9.028193400136014e-08,
 k_(0, 0, 3, 4): 2.64977476293992e-05,
 k_(1, 3, 4, 4): -1.0532892300158684e-07,
 k_(1, 1, 3, 4): 1.8688360338281553e-05,
 k_(2, 3, 4, 4): 0.00015853507610638843,
 k_(2, 3, 3, 4): -2.679868740940373e-05,
 k_(2, 2, 3, 4): 3.736167368756288e-05,
 k_(0, 1, 5, 5): -5.416916040081609e-07,
 k_(0, 0, 1, 5): 1.8658266360281095e-06,
 k_(0, 2, 5, 5): -6.018795600090677e-08,
 k_(1, 2, 5, 5): -2.4075182400362713e-07,
 k_(1, 2, 2, 5): 2.554978732238492e-05,
 k_(0, 3, 5, 5): -1.2037591200181354e-07,
 k_(1, 3, 5, 5): 1.2037591200181354e-07,
 k_(1, 3, 3, 5): 1.3000598496195863e-05,
 k_(2, 3, 5, 5): 0.00021599952709825418,
 k_(0, 4, 5, 5): 7.373024610111077e-07,
 k_(0, 4, 4, 5): -1.670215779025163e-06,
 k_(1, 4, 5, 5): -1.805638680027203e-07,
 k_(1, 4, 4, 5): 1.023195252015415e-06,
 k_(2, 4, 5, 5): 0.0001412460857451279,
 k_(2, 4, 4, 5): 2.407518240036271e-07,
 k_(3, 4, 5, 5): -0.00012022544211181125,
 k_(3, 4, 4, 5): -1.3542290100204023e-07}

[12]:

hamiltonian_sop = pympo.SumOfProducts([])
hamiltonian_sop += kinetic_sop
hamiltonian_sop += potential_sop
hamiltonian_sop = hamiltonian_sop.simplify()
hamiltonian_sop.symbol

[12]:

$\displaystyle k_{(0, 0)} q^2_{0} + k_{(0, 0, 0, 0)} q^4_{0} + k_{(0, 0, 0, 1)} q^3_{0} q^1_{1} + k_{(0, 0, 0, 4)} q^3_{0} q^1_{4} + k_{(0, 0, 0, 5)} q^3_{0} q^1_{5} + k_{(0, 0, 1, 1)} q^2_{0} q^2_{1} + k_{(0, 0, 1, 5)} q^2_{0} q^1_{1} q^1_{5} + k_{(0, 0, 2)} q^2_{0} q^1_{2} + k_{(0, 0, 2, 2)} q^2_{0} q^2_{2} + k_{(0, 0, 2, 3)} q^2_{0} q^1_{2} q^1_{3} + k_{(0, 0, 2, 4)} q^2_{0} q^1_{2} q^1_{4} + k_{(0, 0, 3)} q^2_{0} q^1_{3} + k_{(0, 0, 3, 3)} q^2_{0} q^2_{3} + k_{(0, 0, 3, 4)} q^2_{0} q^1_{3} q^1_{4} + k_{(0, 0, 4)} q^2_{0} q^1_{4} + k_{(0, 0, 4, 4)} q^2_{0} q^2_{4} + k_{(0, 0, 5, 5)} q^2_{0} q^2_{5} + k_{(0, 1, 1, 1)} q^1_{0} q^3_{1} + k_{(0, 1, 1, 2)} q^1_{0} q^2_{1} q^1_{2} + k_{(0, 1, 1, 3)} q^1_{0} q^2_{1} q^1_{3} + k_{(0, 1, 1, 4)} q^1_{0} q^2_{1} q^1_{4} + k_{(0, 1, 2, 2)} q^1_{0} q^1_{1} q^2_{2} + k_{(0, 1, 3, 3)} q^1_{0} q^1_{1} q^2_{3} + k_{(0, 1, 4)} q^1_{0} q^1_{1} q^1_{4} + k_{(0, 1, 4, 4)} q^1_{0} q^1_{1} q^2_{4} + k_{(0, 1, 5)} q^1_{0} q^1_{1} q^1_{5} + k_{(0, 1, 5, 5)} q^1_{0} q^1_{1} q^2_{5} + k_{(0, 2, 2, 4)} q^1_{0} q^2_{2} q^1_{4} + k_{(0, 2, 4, 4)} q^1_{0} q^1_{2} q^2_{4} + k_{(0, 2, 5)} q^1_{0} q^1_{2} q^1_{5} + k_{(0, 2, 5, 5)} q^1_{0} q^1_{2} q^2_{5} + k_{(0, 3, 3)} q^1_{0} q^2_{3} + k_{(0, 3, 3, 3)} q^1_{0} q^3_{3} + k_{(0, 3, 4)} q^1_{0} q^1_{3} q^1_{4} + k_{(0, 3, 4, 4)} q^1_{0} q^1_{3} q^2_{4} + k_{(0, 3, 5)} q^1_{0} q^1_{3} q^1_{5} + k_{(0, 3, 5, 5)} q^1_{0} q^1_{3} q^2_{5} + k_{(0, 4, 4)} q^1_{0} q^2_{4} + k_{(0, 4, 4, 4)} q^1_{0} q^3_{4} + k_{(0, 4, 4, 5)} q^1_{0} q^2_{4} q^1_{5} + k_{(0, 4, 5, 5)} q^1_{0} q^1_{4} q^2_{5} + k_{(0, 5, 5)} q^1_{0} q^2_{5} + k_{(0, 5, 5, 5)} q^1_{0} q^3_{5} + k_{(1, 1)} q^2_{1} + k_{(1, 1, 1, 1)} q^4_{1} + k_{(1, 1, 1, 5)} q^3_{1} q^1_{5} + k_{(1, 1, 2)} q^2_{1} q^1_{2} + k_{(1, 1, 2, 2)} q^2_{1} q^2_{2} + k_{(1, 1, 2, 3)} q^2_{1} q^1_{2} q^1_{3} + k_{(1, 1, 2, 4)} q^2_{1} q^1_{2} q^1_{4} + k_{(1, 1, 3)} q^2_{1} q^1_{3} + k_{(1, 1, 3, 3)} q^2_{1} q^2_{3} + k_{(1, 1, 3, 4)} q^2_{1} q^1_{3} q^1_{4} + k_{(1, 1, 4)} q^2_{1} q^1_{4} + k_{(1, 1, 4, 4)} q^2_{1} q^2_{4} + k_{(1, 1, 5, 5)} q^2_{1} q^2_{5} + k_{(1, 2, 2, 5)} q^1_{1} q^2_{2} q^1_{5} + k_{(1, 2, 4, 4)} q^1_{1} q^1_{2} q^2_{4} + k_{(1, 2, 5)} q^1_{1} q^1_{2} q^1_{5} + k_{(1, 2, 5, 5)} q^1_{1} q^1_{2} q^2_{5} + k_{(1, 3, 3, 5)} q^1_{1} q^2_{3} q^1_{5} + k_{(1, 3, 4, 4)} q^1_{1} q^1_{3} q^2_{4} + k_{(1, 3, 5)} q^1_{1} q^1_{3} q^1_{5} + k_{(1, 3, 5, 5)} q^1_{1} q^1_{3} q^2_{5} + k_{(1, 4, 4, 4)} q^1_{1} q^3_{4} + k_{(1, 4, 4, 5)} q^1_{1} q^2_{4} q^1_{5} + k_{(1, 4, 5)} q^1_{1} q^1_{4} q^1_{5} + k_{(1, 4, 5, 5)} q^1_{1} q^1_{4} q^2_{5} + k_{(1, 5, 5, 5)} q^1_{1} q^3_{5} + k_{(2, 2)} q^2_{2} + k_{(2, 2, 2)} q^3_{2} + k_{(2, 2, 2, 2)} q^4_{2} + k_{(2, 2, 2, 3)} q^3_{2} q^1_{3} + k_{(2, 2, 2, 4)} q^3_{2} q^1_{4} + k_{(2, 2, 3)} q^2_{2} q^1_{3} + k_{(2, 2, 3, 3)} q^2_{2} q^2_{3} + k_{(2, 2, 3, 4)} q^2_{2} q^1_{3} q^1_{4} + k_{(2, 2, 4)} q^2_{2} q^1_{4} + k_{(2, 2, 4, 4)} q^2_{2} q^2_{4} + k_{(2, 2, 5, 5)} q^2_{2} q^2_{5} + k_{(2, 3, 3)} q^1_{2} q^2_{3} + k_{(2, 3, 3, 3)} q^1_{2} q^3_{3} + k_{(2, 3, 3, 4)} q^1_{2} q^2_{3} q^1_{4} + k_{(2, 3, 4)} q^1_{2} q^1_{3} q^1_{4} + k_{(2, 3, 4, 4)} q^1_{2} q^1_{3} q^2_{4} + k_{(2, 3, 5, 5)} q^1_{2} q^1_{3} q^2_{5} + k_{(2, 4, 4)} q^1_{2} q^2_{4} + k_{(2, 4, 4, 4)} q^1_{2} q^3_{4} + k_{(2, 4, 4, 5)} q^1_{2} q^2_{4} q^1_{5} + k_{(2, 4, 5, 5)} q^1_{2} q^1_{4} q^2_{5} + k_{(2, 5, 5)} q^1_{2} q^2_{5} + k_{(3, 3)} q^2_{3} + k_{(3, 3, 3)} q^3_{3} + k_{(3, 3, 3, 3)} q^4_{3} + k_{(3, 3, 3, 4)} q^3_{3} q^1_{4} + k_{(3, 3, 4)} q^2_{3} q^1_{4} + k_{(3, 3, 4, 4)} q^2_{3} q^2_{4} + k_{(3, 3, 5, 5)} q^2_{3} q^2_{5} + k_{(3, 4, 4)} q^1_{3} q^2_{4} + k_{(3, 4, 4, 4)} q^1_{3} q^3_{4} + k_{(3, 4, 4, 5)} q^1_{3} q^2_{4} q^1_{5} + k_{(3, 4, 5, 5)} q^1_{3} q^1_{4} q^2_{5} + k_{(3, 5, 5)} q^1_{3} q^2_{5} + k_{(4, 4)} q^2_{4} + k_{(4, 4, 4)} q^3_{4} + k_{(4, 4, 4, 4)} q^4_{4} + k_{(4, 4, 4, 5)} q^3_{4} q^1_{5} + k_{(4, 4, 5)} q^2_{4} q^1_{5} + k_{(4, 4, 5, 5)} q^2_{4} q^2_{5} + k_{(4, 5, 5)} q^1_{4} q^2_{5} + k_{(4, 5, 5, 5)} q^1_{4} q^3_{5} + k_{(5, 5)} q^2_{5} + k_{(5, 5, 5)} q^3_{5} + k_{(5, 5, 5, 5)} q^4_{5} - 0.5 \frac{\partial}{\partial q^2_{0}} - 0.5 \frac{\partial}{\partial q^2_{1}} - 0.5 \frac{\partial}{\partial q^2_{2}} - 0.5 \frac{\partial}{\partial q^2_{3}} - 0.5 \frac{\partial}{\partial q^2_{4}} - 0.5 \frac{\partial}{\partial q^2_{5}}$

[13]:

%time am_hamiltonian = pympo.AssignManager(hamiltonian_sop)
%time am_hamiltonian.assign(keep_symbol=False)  # This part takes time due to using Sympy
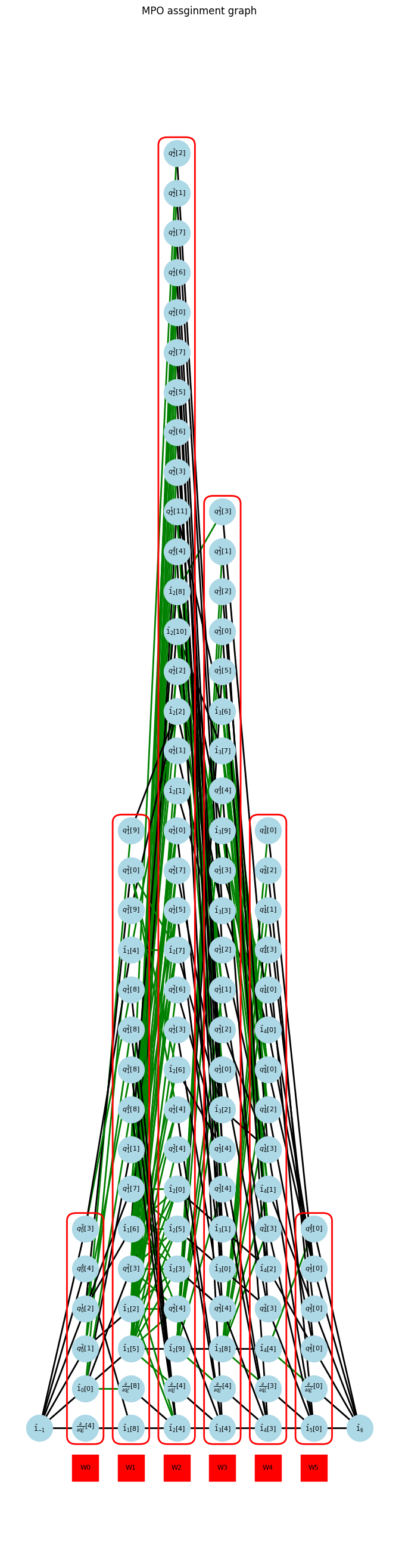
am_hamiltonian.show_graph()
display(*am_hamiltonian.Wsym)
# %time potential_mpo = am_potential.numerical_mpo()
hamiltonian_mpo = am_hamiltonian.numerical_mpo(subs=coef_symbol)

2024-12-31 18:07:40.603 | INFO     | pympo.bipartite:assign:286 - assigned 1/6
2024-12-31 18:07:40.607 | INFO     | pympo.bipartite:assign:286 - assigned 2/6
2024-12-31 18:07:40.611 | INFO     | pympo.bipartite:assign:286 - assigned 3/6
2024-12-31 18:07:40.615 | INFO     | pympo.bipartite:assign:286 - assigned 4/6
2024-12-31 18:07:40.618 | INFO     | pympo.bipartite:assign:286 - assigned 5/6
2024-12-31 18:07:40.620 | INFO     | pympo.bipartite:assign:286 - assigned 6/6

CPU times: user 65 μs, sys: 0 ns, total: 65 μs
Wall time: 67 μs
CPU times: user 23.5 ms, sys: 1.27 ms, total: 24.8 ms
Wall time: 24.4 ms

../_images/example_pytdscf-taylor_14_2.png

$\displaystyle \left[\begin{matrix}1 & q^2_{0} & q^1_{0} & q^3_{0} & k_{(0, 0, 0, 0)} q^4_{0} - 0.5 \frac{\partial}{\partial q^2_{0}}\end{matrix}\right]$

$\displaystyle \left[\begin{matrix}0 & q^1_{1} & 0 & q^2_{1} & 0 & 1 & 0 & 0 & k_{(1, 1, 1, 1)} q^4_{1} - 0.5 \frac{\partial}{\partial q^2_{1}} & k_{(1, 1, 1, 5)} q^3_{1}\\0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & k_{(0, 0, 1, 1)} q^2_{1} & k_{(0, 0, 1, 5)} q^1_{1}\\q^2_{1} & 0 & 0 & 0 & 0 & 0 & 1 & q^1_{1} & k_{(0, 1, 1, 1)} q^3_{1} & 0\\0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & k_{(0, 0, 0, 1)} q^1_{1} & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\end{matrix}\right]$

$\displaystyle \left[\begin{array}{cccccccccccc}0 & 0 & 0 & 0 & k_{(0, 1, 1, 2)} q^1_{2} & 0 & k_{(0, 1, 1, 3)} & k_{(0, 1, 1, 4)} & 0 & 0 & 0 & 0\\k_{(1, 2, 5, 5)} q^1_{2} & 0 & k_{(1, 2, 2, 5)} q^2_{2} + k_{(1, 2, 5)} q^1_{2} & 0 & 0 & k_{(1, 2, 4, 4)} q^1_{2} & 0 & 0 & 1 & 0 & 0 & 0\\k_{(0, 0, 5, 5)} & k_{(0, 0, 3, 4)} & 0 & k_{(0, 0, 3, 3)} & k_{(0, 0)} + k_{(0, 0, 2)} q^1_{2} + k_{(0, 0, 2, 2)} q^2_{2} & k_{(0, 0, 4, 4)} & k_{(0, 0, 2, 3)} q^1_{2} + k_{(0, 0, 3)} & k_{(0, 0, 2, 4)} q^1_{2} + k_{(0, 0, 4)} & 0 & 0 & 0 & 0\\k_{(1, 1, 5, 5)} & k_{(1, 1, 3, 4)} & 0 & k_{(1, 1, 3, 3)} & k_{(1, 1)} + k_{(1, 1, 2)} q^1_{2} + k_{(1, 1, 2, 2)} q^2_{2} & k_{(1, 1, 4, 4)} & k_{(1, 1, 2, 3)} q^1_{2} + k_{(1, 1, 3)} & k_{(1, 1, 2, 4)} q^1_{2} + k_{(1, 1, 4)} & 0 & 0 & 0 & 0\\0 & 0 & k_{(0, 0, 0, 5)} & 0 & 0 & 0 & 0 & k_{(0, 0, 0, 4)} & 0 & 0 & 0 & 0\\k_{(2, 2, 5, 5)} q^2_{2} + k_{(2, 5, 5)} q^1_{2} + k_{(5, 5)} & k_{(2, 2, 3, 4)} q^2_{2} + k_{(2, 3, 4)} q^1_{2} & 0 & k_{(2, 2, 3, 3)} q^2_{2} + k_{(2, 3, 3)} q^1_{2} + k_{(3, 3)} & k_{(2, 2)} q^2_{2} + k_{(2, 2, 2)} q^3_{2} + k_{(2, 2, 2, 2)} q^4_{2} - 0.5 \frac{\partial}{\partial q^2_{2}} & k_{(2, 2, 4, 4)} q^2_{2} + k_{(2, 4, 4)} q^1_{2} + k_{(4, 4)} & k_{(2, 2, 2, 3)} q^3_{2} + k_{(2, 2, 3)} q^2_{2} & k_{(2, 2, 2, 4)} q^3_{2} + k_{(2, 2, 4)} q^2_{2} & 0 & 1 & 0 & q^1_{2}\\k_{(0, 2, 5, 5)} q^1_{2} + k_{(0, 5, 5)} & k_{(0, 3, 4)} & k_{(0, 2, 5)} q^1_{2} & k_{(0, 3, 3)} & 0 & k_{(0, 2, 4, 4)} q^1_{2} + k_{(0, 4, 4)} & 0 & k_{(0, 2, 2, 4)} q^2_{2} & 0 & 0 & 1 & 0\\k_{(0, 1, 5, 5)} & 0 & k_{(0, 1, 5)} & k_{(0, 1, 3, 3)} & k_{(0, 1, 2, 2)} q^2_{2} & k_{(0, 1, 4, 4)} & 0 & k_{(0, 1, 4)} & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\end{array}\right]$

$\displaystyle \left[\begin{matrix}0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & q^1_{3} & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & q^2_{3} & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & q^1_{3} & 0 & 0 & 0 & 0 & 0\\0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\k_{(1, 3, 4, 4)} q^1_{3} & k_{(1, 3, 5, 5)} q^1_{3} & 0 & k_{(1, 3, 3, 5)} q^2_{3} + k_{(1, 3, 5)} q^1_{3} & 0 & 0 & 0 & 0 & 0 & 1\\k_{(3, 3, 4, 4)} q^2_{3} + k_{(3, 4, 4)} q^1_{3} & k_{(3, 3, 5, 5)} q^2_{3} + k_{(3, 5, 5)} q^1_{3} & k_{(3, 3, 3, 4)} q^3_{3} + k_{(3, 3, 4)} q^2_{3} & 0 & k_{(3, 3, 3)} q^3_{3} + k_{(3, 3, 3, 3)} q^4_{3} - 0.5 \frac{\partial}{\partial q^2_{3}} & q^1_{3} & 0 & 0 & 1 & 0\\k_{(0, 3, 4, 4)} q^1_{3} & k_{(0, 3, 5, 5)} q^1_{3} & 0 & k_{(0, 3, 5)} q^1_{3} & k_{(0, 3, 3, 3)} q^3_{3} & 0 & 0 & 1 & 0 & 0\\k_{(2, 3, 4, 4)} q^1_{3} & k_{(2, 3, 5, 5)} q^1_{3} & k_{(2, 3, 3, 4)} q^2_{3} & 0 & k_{(2, 3, 3, 3)} q^3_{3} & 0 & 1 & 0 & 0 & 0\end{matrix}\right]$

$\displaystyle \left[\begin{matrix}0 & 0 & 0 & q^2_{4} & 0\\0 & 0 & 1 & 0 & 0\\0 & 0 & 0 & q^1_{4} & 0\\1 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 1 & 0\\k_{(3, 4, 4, 5)} q^2_{4} & 0 & k_{(3, 4, 5, 5)} q^1_{4} & k_{(3, 4, 4, 4)} q^3_{4} & 0\\k_{(2, 4, 4, 5)} q^2_{4} & 0 & k_{(2, 4, 5, 5)} q^1_{4} & k_{(2, 4, 4, 4)} q^3_{4} & 0\\k_{(0, 4, 4, 5)} q^2_{4} & k_{(0, 5, 5, 5)} & k_{(0, 4, 5, 5)} q^1_{4} & k_{(0, 4, 4, 4)} q^3_{4} & 0\\k_{(4, 4, 4, 5)} q^3_{4} + k_{(4, 4, 5)} q^2_{4} & k_{(4, 5, 5, 5)} q^1_{4} + k_{(5, 5, 5)} & k_{(4, 4, 5, 5)} q^2_{4} + k_{(4, 5, 5)} q^1_{4} & k_{(4, 4, 4)} q^3_{4} + k_{(4, 4, 4, 4)} q^4_{4} - 0.5 \frac{\partial}{\partial q^2_{4}} & 1\\k_{(1, 4, 4, 5)} q^2_{4} + k_{(1, 4, 5)} q^1_{4} & k_{(1, 5, 5, 5)} & k_{(1, 4, 5, 5)} q^1_{4} & k_{(1, 4, 4, 4)} q^3_{4} & 0\end{matrix}\right]$

$\displaystyle \left[\begin{matrix}q^1_{5}\\q^3_{5}\\q^2_{5}\\1\\k_{(5, 5, 5, 5)} q^4_{5} - 0.5 \frac{\partial}{\partial q^2_{5}}\end{matrix}\right]$

[14]:

display(*sympy.Mul(*am_hamiltonian.Wsym).expand())
display(hamiltonian_sop.symbol.expand())

assert sympy.Mul(*am_hamiltonian.Wsym)[0].expand() == hamiltonian_sop.symbol, (
    sympy.Mul(*am_hamiltonian.Wsym)[0].expand() - hamiltonian_sop.symbol
)

$\displaystyle k_{(0, 0)} q^2_{0} + k_{(0, 0, 0, 0)} q^4_{0} + k_{(0, 0, 0, 1)} q^3_{0} q^1_{1} + k_{(0, 0, 0, 4)} q^3_{0} q^1_{4} + k_{(0, 0, 0, 5)} q^3_{0} q^1_{5} + k_{(0, 0, 1, 1)} q^2_{0} q^2_{1} + k_{(0, 0, 1, 5)} q^2_{0} q^1_{1} q^1_{5} + k_{(0, 0, 2)} q^2_{0} q^1_{2} + k_{(0, 0, 2, 2)} q^2_{0} q^2_{2} + k_{(0, 0, 2, 3)} q^2_{0} q^1_{2} q^1_{3} + k_{(0, 0, 2, 4)} q^2_{0} q^1_{2} q^1_{4} + k_{(0, 0, 3)} q^2_{0} q^1_{3} + k_{(0, 0, 3, 3)} q^2_{0} q^2_{3} + k_{(0, 0, 3, 4)} q^2_{0} q^1_{3} q^1_{4} + k_{(0, 0, 4)} q^2_{0} q^1_{4} + k_{(0, 0, 4, 4)} q^2_{0} q^2_{4} + k_{(0, 0, 5, 5)} q^2_{0} q^2_{5} + k_{(0, 1, 1, 1)} q^1_{0} q^3_{1} + k_{(0, 1, 1, 2)} q^1_{0} q^2_{1} q^1_{2} + k_{(0, 1, 1, 3)} q^1_{0} q^2_{1} q^1_{3} + k_{(0, 1, 1, 4)} q^1_{0} q^2_{1} q^1_{4} + k_{(0, 1, 2, 2)} q^1_{0} q^1_{1} q^2_{2} + k_{(0, 1, 3, 3)} q^1_{0} q^1_{1} q^2_{3} + k_{(0, 1, 4)} q^1_{0} q^1_{1} q^1_{4} + k_{(0, 1, 4, 4)} q^1_{0} q^1_{1} q^2_{4} + k_{(0, 1, 5)} q^1_{0} q^1_{1} q^1_{5} + k_{(0, 1, 5, 5)} q^1_{0} q^1_{1} q^2_{5} + k_{(0, 2, 2, 4)} q^1_{0} q^2_{2} q^1_{4} + k_{(0, 2, 4, 4)} q^1_{0} q^1_{2} q^2_{4} + k_{(0, 2, 5)} q^1_{0} q^1_{2} q^1_{5} + k_{(0, 2, 5, 5)} q^1_{0} q^1_{2} q^2_{5} + k_{(0, 3, 3)} q^1_{0} q^2_{3} + k_{(0, 3, 3, 3)} q^1_{0} q^3_{3} + k_{(0, 3, 4)} q^1_{0} q^1_{3} q^1_{4} + k_{(0, 3, 4, 4)} q^1_{0} q^1_{3} q^2_{4} + k_{(0, 3, 5)} q^1_{0} q^1_{3} q^1_{5} + k_{(0, 3, 5, 5)} q^1_{0} q^1_{3} q^2_{5} + k_{(0, 4, 4)} q^1_{0} q^2_{4} + k_{(0, 4, 4, 4)} q^1_{0} q^3_{4} + k_{(0, 4, 4, 5)} q^1_{0} q^2_{4} q^1_{5} + k_{(0, 4, 5, 5)} q^1_{0} q^1_{4} q^2_{5} + k_{(0, 5, 5)} q^1_{0} q^2_{5} + k_{(0, 5, 5, 5)} q^1_{0} q^3_{5} + k_{(1, 1)} q^2_{1} + k_{(1, 1, 1, 1)} q^4_{1} + k_{(1, 1, 1, 5)} q^3_{1} q^1_{5} + k_{(1, 1, 2)} q^2_{1} q^1_{2} + k_{(1, 1, 2, 2)} q^2_{1} q^2_{2} + k_{(1, 1, 2, 3)} q^2_{1} q^1_{2} q^1_{3} + k_{(1, 1, 2, 4)} q^2_{1} q^1_{2} q^1_{4} + k_{(1, 1, 3)} q^2_{1} q^1_{3} + k_{(1, 1, 3, 3)} q^2_{1} q^2_{3} + k_{(1, 1, 3, 4)} q^2_{1} q^1_{3} q^1_{4} + k_{(1, 1, 4)} q^2_{1} q^1_{4} + k_{(1, 1, 4, 4)} q^2_{1} q^2_{4} + k_{(1, 1, 5, 5)} q^2_{1} q^2_{5} + k_{(1, 2, 2, 5)} q^1_{1} q^2_{2} q^1_{5} + k_{(1, 2, 4, 4)} q^1_{1} q^1_{2} q^2_{4} + k_{(1, 2, 5)} q^1_{1} q^1_{2} q^1_{5} + k_{(1, 2, 5, 5)} q^1_{1} q^1_{2} q^2_{5} + k_{(1, 3, 3, 5)} q^1_{1} q^2_{3} q^1_{5} + k_{(1, 3, 4, 4)} q^1_{1} q^1_{3} q^2_{4} + k_{(1, 3, 5)} q^1_{1} q^1_{3} q^1_{5} + k_{(1, 3, 5, 5)} q^1_{1} q^1_{3} q^2_{5} + k_{(1, 4, 4, 4)} q^1_{1} q^3_{4} + k_{(1, 4, 4, 5)} q^1_{1} q^2_{4} q^1_{5} + k_{(1, 4, 5)} q^1_{1} q^1_{4} q^1_{5} + k_{(1, 4, 5, 5)} q^1_{1} q^1_{4} q^2_{5} + k_{(1, 5, 5, 5)} q^1_{1} q^3_{5} + k_{(2, 2)} q^2_{2} + k_{(2, 2, 2)} q^3_{2} + k_{(2, 2, 2, 2)} q^4_{2} + k_{(2, 2, 2, 3)} q^3_{2} q^1_{3} + k_{(2, 2, 2, 4)} q^3_{2} q^1_{4} + k_{(2, 2, 3)} q^2_{2} q^1_{3} + k_{(2, 2, 3, 3)} q^2_{2} q^2_{3} + k_{(2, 2, 3, 4)} q^2_{2} q^1_{3} q^1_{4} + k_{(2, 2, 4)} q^2_{2} q^1_{4} + k_{(2, 2, 4, 4)} q^2_{2} q^2_{4} + k_{(2, 2, 5, 5)} q^2_{2} q^2_{5} + k_{(2, 3, 3)} q^1_{2} q^2_{3} + k_{(2, 3, 3, 3)} q^1_{2} q^3_{3} + k_{(2, 3, 3, 4)} q^1_{2} q^2_{3} q^1_{4} + k_{(2, 3, 4)} q^1_{2} q^1_{3} q^1_{4} + k_{(2, 3, 4, 4)} q^1_{2} q^1_{3} q^2_{4} + k_{(2, 3, 5, 5)} q^1_{2} q^1_{3} q^2_{5} + k_{(2, 4, 4)} q^1_{2} q^2_{4} + k_{(2, 4, 4, 4)} q^1_{2} q^3_{4} + k_{(2, 4, 4, 5)} q^1_{2} q^2_{4} q^1_{5} + k_{(2, 4, 5, 5)} q^1_{2} q^1_{4} q^2_{5} + k_{(2, 5, 5)} q^1_{2} q^2_{5} + k_{(3, 3)} q^2_{3} + k_{(3, 3, 3)} q^3_{3} + k_{(3, 3, 3, 3)} q^4_{3} + k_{(3, 3, 3, 4)} q^3_{3} q^1_{4} + k_{(3, 3, 4)} q^2_{3} q^1_{4} + k_{(3, 3, 4, 4)} q^2_{3} q^2_{4} + k_{(3, 3, 5, 5)} q^2_{3} q^2_{5} + k_{(3, 4, 4)} q^1_{3} q^2_{4} + k_{(3, 4, 4, 4)} q^1_{3} q^3_{4} + k_{(3, 4, 4, 5)} q^1_{3} q^2_{4} q^1_{5} + k_{(3, 4, 5, 5)} q^1_{3} q^1_{4} q^2_{5} + k_{(3, 5, 5)} q^1_{3} q^2_{5} + k_{(4, 4)} q^2_{4} + k_{(4, 4, 4)} q^3_{4} + k_{(4, 4, 4, 4)} q^4_{4} + k_{(4, 4, 4, 5)} q^3_{4} q^1_{5} + k_{(4, 4, 5)} q^2_{4} q^1_{5} + k_{(4, 4, 5, 5)} q^2_{4} q^2_{5} + k_{(4, 5, 5)} q^1_{4} q^2_{5} + k_{(4, 5, 5, 5)} q^1_{4} q^3_{5} + k_{(5, 5)} q^2_{5} + k_{(5, 5, 5)} q^3_{5} + k_{(5, 5, 5, 5)} q^4_{5} - 0.5 \frac{\partial}{\partial q^2_{0}} - 0.5 \frac{\partial}{\partial q^2_{1}} - 0.5 \frac{\partial}{\partial q^2_{2}} - 0.5 \frac{\partial}{\partial q^2_{3}} - 0.5 \frac{\partial}{\partial q^2_{4}} - 0.5 \frac{\partial}{\partial q^2_{5}}$

[15]:

H = {
    tuple([(idof, idof) for idof in range(f)]): TensorOperator(mpo=hamiltonian_mpo)
}
hamiltonian = [[H]]


H = TensorHamiltonian(f, potential=hamiltonian, kinetic=None, backend=backend) # because kinetic term is absorbed into potential
operators = {"hamiltonian": H}

[16]:

model = Model(basinfo=basinfo, operators=operators)
model.m_aux_max = m
model.init_HartreeProduct = [
    [
        [1.0] + [0.0] * (N-1) for _ in range(f)
    ]
]

[17]:

jobname = "ch2o-mpo"
simulator = Simulator(jobname=jobname, model=model, backend=backend)
import time
start = time.time()
ener, wf = simulator.relax(savefile_ext="_gs", maxstep=10, stepsize=0.1)#.(maxstep=100, stepsize=Δt)
end = time.time()
print(end-start)
ener * units.au_in_eV

2024-12-31 18:07:41,817 - INFO:main.pytdscf._const_cls - 
     ____     __________   .____ ____   _____
    / _  |   /__  __/ _ \ / ___ / _  \ / ___/
   / /_) /_  __/ / / / ||/ /__ / / )_// /__
  /  ___/ / / / / / / / |.__  / |  __/ ___/
 /  /  / /_/ / / / /_/ /___/ /| \_/ / /
/__/   \__, /_/ /_____/_____/ \____/_/
      /____/

2024-12-31 18:07:41,817 - INFO:main.pytdscf._const_cls - Log file is ./ch2o-mpo_relax/main.log
2024-12-31 18:07:41,817 - INFO:main.pytdscf.simulator_cls - Set integral of DVR basis
2024-12-31 18:07:41,821 - INFO:main.pytdscf.simulator_cls - Set initial wave function (DVR basis)
2024-12-31 18:07:41,821 - INFO:main.pytdscf.simulator_cls - Prepare MPS w.f.
2024-12-31 18:07:41,822 - INFO:main.pytdscf._mps_cls - Initial MPS: 0-state with weights 1.0
2024-12-31 18:07:42,324 - INFO:main.pytdscf.simulator_cls - Wave function is saved in wf_ch2o-mpo_gs.pkl
2024-12-31 18:07:42,325 - INFO:main.pytdscf.simulator_cls - Start initial step    0.000 [fs]
2024-12-31 18:07:44,635 - INFO:main.pytdscf.simulator_cls - End     0 step; propagated    0.100 [fs]; AVG Krylov iteration: 17.17
2024-12-31 18:07:45,896 - INFO:main.pytdscf.simulator_cls - Saved wavefunction    0.900 [fs]
2024-12-31 18:07:46,016 - INFO:main.pytdscf.simulator_cls - End     9 step; propagated    0.900 [fs]; AVG Krylov iteration: 3.00
2024-12-31 18:07:46,017 - INFO:main.pytdscf.simulator_cls - End simulation and save wavefunction
2024-12-31 18:07:46,020 - INFO:main.pytdscf.simulator_cls - Wave function is saved in wf_ch2o-mpo_gs.pkl

4.204995155334473

[17]:

0.7088296546418331

[18]:

!tail ch2o-mpo_relax/main.log

| pop 1.0000 | ene[eV]:  0.7088297 | time[fs]:    0.400 | elapsed[sec]:     2.21
| pop 1.0000 | ene[eV]:  0.7088297 | time[fs]:    0.500 | elapsed[sec]:     2.32
| pop 1.0000 | ene[eV]:  0.7088297 | time[fs]:    0.600 | elapsed[sec]:     2.43
| pop 1.0000 | ene[eV]:  0.7088297 | time[fs]:    0.700 | elapsed[sec]:     2.53
| pop 1.0000 | ene[eV]:  0.7088297 | time[fs]:    0.800 | elapsed[sec]:     2.62
Saved wavefunction    0.900 [fs]
| pop 1.0000 | ene[eV]:  0.7088297 | time[fs]:    0.900 | elapsed[sec]:     2.71
End     9 step; propagated    0.900 [fs]; AVG Krylov iteration: 3.00
End simulation and save wavefunction
Wave function is saved in wf_ch2o-mpo_gs.pkl

/opt/homebrew/Cellar/python@3.12/3.12.2_1/Frameworks/Python.framework/Versions/3.12/lib/python3.12/pty.py:95: RuntimeWarning: os.fork() was called. os.fork() is incompatible with multithreaded code, and JAX is multithreaded, so this will likely lead to a deadlock.
  pid, fd = os.forkpty()

Confirm with SOP model

[19]:

from discvar import PrimBas_HO

prim_info = [
    [
        PrimBas_HO(0.0, omega, nprim)
        for nprim, omega in zip(nprims, freqs, strict=True)
    ]
]
nstate = len(
    prim_info
)  # len(prim_info) is number of state, in this case state is S0
ndof = len(prim_info[0])  # Number of degree of freedom, H2O has 3 DOFs
basinfo = BasInfo(prim_info, spf_info=None)  # Set basis information object
from pytdscf.hamiltonian_cls import read_potential_nMR

hamiltonian = read_potential_nMR(k_orig, cut_off=cutoff)
operators = {"hamiltonian": hamiltonian}

model = Model(basinfo, operators)
model.m_aux_max = m
model.init_HartreeProduct = [
    [
        [1.0] + [0.0] * (N-1) for _ in range(f)
    ]
]
jobname = "ch2o-sop"
simulator = Simulator(jobname, model, ci_type="MPS", backend="Numpy")

start = time.time()
ener, wf = simulator.relax(savefile_ext="_gs", maxstep=10, stepsize=0.1)
end = time.time()
print(end-start)
ener * units.au_in_eV

2024-12-31 18:07:46,157 - INFO:main.pytdscf.model_cls - The layer of SPF is not used.
2024-12-31 18:07:46,159 - INFO:main.pytdscf.hamiltonian_cls - Construct anharmonic polynomial operator
2024-12-31 18:07:46,160 - WARNING:main.pytdscf._const_cls - rebind const jobname
2024-12-31 18:07:46,162 - WARNING:main.pytdscf._const_cls - rebind const logger
2024-12-31 18:07:46,162 - WARNING:main.pytdscf._const_cls - rebind const logger
2024-12-31 18:07:46,162 - INFO:main.pytdscf._const_cls - 
     ____     __________   .____ ____   _____
    / _  |   /__  __/ _ \ / ___ / _  \ / ___/
   / /_) /_  __/ / / / ||/ /__ / / )_// /__
  /  ___/ / / / / / / / |.__  / |  __/ ___/
 /  /  / /_/ / / / /_/ /___/ /| \_/ / /
/__/   \__, /_/ /_____/_____/ \____/_/
      /____/

2024-12-31 18:07:46,162 - INFO:main.pytdscf._const_cls - 
     ____     __________   .____ ____   _____
    / _  |   /__  __/ _ \ / ___ / _  \ / ___/
   / /_) /_  __/ / / / ||/ /__ / / )_// /__
  /  ___/ / / / / / / / |.__  / |  __/ ___/
 /  /  / /_/ / / / /_/ /___/ /| \_/ / /
/__/   \__, /_/ /_____/_____/ \____/_/
      /____/

2024-12-31 18:07:46,163 - INFO:main.pytdscf._const_cls - Log file is ./ch2o-sop_relax/main.log
2024-12-31 18:07:46,163 - INFO:main.pytdscf._const_cls - Log file is ./ch2o-sop_relax/main.log
2024-12-31 18:07:46,164 - WARNING:main.pytdscf._const_cls - rebind const doRestart
2024-12-31 18:07:46,164 - WARNING:main.pytdscf._const_cls - rebind const doRestart
2024-12-31 18:07:46,164 - WARNING:main.pytdscf._const_cls - rebind const doRelax
2024-12-31 18:07:46,164 - WARNING:main.pytdscf._const_cls - rebind const doRelax
2024-12-31 18:07:46,165 - WARNING:main.pytdscf._const_cls - rebind const doAppDipo
2024-12-31 18:07:46,165 - WARNING:main.pytdscf._const_cls - rebind const doAppDipo
2024-12-31 18:07:46,166 - WARNING:main.pytdscf._const_cls - rebind const doDVR
2024-12-31 18:07:46,166 - WARNING:main.pytdscf._const_cls - rebind const doDVR
2024-12-31 18:07:46,166 - WARNING:main.pytdscf._const_cls - rebind const savefile_ext
2024-12-31 18:07:46,166 - WARNING:main.pytdscf._const_cls - rebind const savefile_ext
2024-12-31 18:07:46,167 - WARNING:main.pytdscf._const_cls - rebind const loadfile_ext
2024-12-31 18:07:46,167 - WARNING:main.pytdscf._const_cls - rebind const loadfile_ext
2024-12-31 18:07:46,167 - WARNING:main.pytdscf._const_cls - rebind const time_fs_init
2024-12-31 18:07:46,167 - WARNING:main.pytdscf._const_cls - rebind const time_fs_init
2024-12-31 18:07:46,168 - WARNING:main.pytdscf._const_cls - rebind const maxstep
2024-12-31 18:07:46,168 - WARNING:main.pytdscf._const_cls - rebind const maxstep
2024-12-31 18:07:46,169 - WARNING:main.pytdscf._const_cls - rebind const doOrtho
2024-12-31 18:07:46,169 - WARNING:main.pytdscf._const_cls - rebind const doOrtho
2024-12-31 18:07:46,170 - WARNING:main.pytdscf._const_cls - rebind const doTDHamil
2024-12-31 18:07:46,170 - WARNING:main.pytdscf._const_cls - rebind const doTDHamil
2024-12-31 18:07:46,171 - WARNING:main.pytdscf._const_cls - rebind const oldcode
2024-12-31 18:07:46,171 - WARNING:main.pytdscf._const_cls - rebind const oldcode
2024-12-31 18:07:46,172 - WARNING:main.pytdscf._const_cls - rebind const use_jax
2024-12-31 18:07:46,172 - WARNING:main.pytdscf._const_cls - rebind const use_jax
2024-12-31 18:07:46,172 - WARNING:main.pytdscf._const_cls - rebind const thresh_exp
2024-12-31 18:07:46,172 - WARNING:main.pytdscf._const_cls - rebind const thresh_exp
2024-12-31 18:07:46,173 - WARNING:main.pytdscf._const_cls - rebind const standard_method
2024-12-31 18:07:46,173 - WARNING:main.pytdscf._const_cls - rebind const standard_method
2024-12-31 18:07:46,174 - WARNING:main.pytdscf._const_cls - rebind const use_mpo
2024-12-31 18:07:46,174 - WARNING:main.pytdscf._const_cls - rebind const use_mpo
2024-12-31 18:07:46,176 - INFO:main.pytdscf.simulator_cls - Set integral of FBR basis
2024-12-31 18:07:46,176 - INFO:main.pytdscf.simulator_cls - Set integral of FBR basis
2024-12-31 18:07:46,216 - INFO:main.pytdscf.simulator_cls - Set initial wave function (FBR basis)
2024-12-31 18:07:46,216 - INFO:main.pytdscf.simulator_cls - Set initial wave function (FBR basis)
2024-12-31 18:07:46,217 - INFO:main.pytdscf.simulator_cls - Prepare MPS w.f.
2024-12-31 18:07:46,217 - INFO:main.pytdscf.simulator_cls - Prepare MPS w.f.
2024-12-31 18:07:46,219 - INFO:main.pytdscf._mps_cls - Initial MPS: 0-state with weights 1.0
2024-12-31 18:07:46,219 - INFO:main.pytdscf._mps_cls - Initial MPS: 0-state with weights 1.0
2024-12-31 18:07:46,228 - INFO:main.pytdscf.simulator_cls - Wave function is saved in wf_ch2o-sop_gs.pkl
2024-12-31 18:07:46,228 - INFO:main.pytdscf.simulator_cls - Wave function is saved in wf_ch2o-sop_gs.pkl
2024-12-31 18:07:46,229 - INFO:main.pytdscf.simulator_cls - Start initial step    0.000 [fs]
2024-12-31 18:07:46,229 - INFO:main.pytdscf.simulator_cls - Start initial step    0.000 [fs]
2024-12-31 18:07:51,299 - INFO:main.pytdscf.simulator_cls - End     0 step; propagated    0.100 [fs]; AVG Krylov iteration: 17.17
2024-12-31 18:07:51,299 - INFO:main.pytdscf.simulator_cls - End     0 step; propagated    0.100 [fs]; AVG Krylov iteration: 17.17
2024-12-31 18:08:00,045 - INFO:main.pytdscf.simulator_cls - Saved wavefunction    0.900 [fs]
2024-12-31 18:08:00,045 - INFO:main.pytdscf.simulator_cls - Saved wavefunction    0.900 [fs]
2024-12-31 18:08:00,814 - INFO:main.pytdscf.simulator_cls - End     9 step; propagated    0.900 [fs]; AVG Krylov iteration: 3.00
2024-12-31 18:08:00,814 - INFO:main.pytdscf.simulator_cls - End     9 step; propagated    0.900 [fs]; AVG Krylov iteration: 3.00
2024-12-31 18:08:00,815 - INFO:main.pytdscf.simulator_cls - End simulation and save wavefunction
2024-12-31 18:08:00,815 - INFO:main.pytdscf.simulator_cls - End simulation and save wavefunction
2024-12-31 18:08:00,832 - INFO:main.pytdscf.simulator_cls - Wave function is saved in wf_ch2o-sop_gs.pkl
2024-12-31 18:08:00,832 - INFO:main.pytdscf.simulator_cls - Wave function is saved in wf_ch2o-sop_gs.pkl

14.673572063446045

[19]:

0.7088296546418337

[20]:

!tail ch2o-sop_relax/main.log

| pop 1.0000 | ene[eV]:  0.7088297 | time[fs]:    0.400 | elapsed[sec]:    12.07
| pop 1.0000 | ene[eV]:  0.7088297 | time[fs]:    0.500 | elapsed[sec]:    13.02
| pop 1.0000 | ene[eV]:  0.7088297 | time[fs]:    0.600 | elapsed[sec]:    13.93
| pop 1.0000 | ene[eV]:  0.7088297 | time[fs]:    0.700 | elapsed[sec]:    14.72
| pop 1.0000 | ene[eV]:  0.7088297 | time[fs]:    0.800 | elapsed[sec]:    15.48
Saved wavefunction    0.900 [fs]
| pop 1.0000 | ene[eV]:  0.7088297 | time[fs]:    0.900 | elapsed[sec]:    16.17
End     9 step; propagated    0.900 [fs]; AVG Krylov iteration: 3.00
End simulation and save wavefunction
Wave function is saved in wf_ch2o-sop_gs.pkl