Learning about Automatic symbolic MPO construction

Reference

Jiajun Ren, Weitang Li, Tong Jiang, Zhigang Shuai; A general automatic method for optimal construction of matrix product operators using bipartite graph theory. J. Chem. Phys. 28 August 2020; 153 (8): 084118.

Import modules

[1]:

import sympy

from pympo import (
    OpSite,
    SumOfProducts,
    assign_core,
    get_UVE,
    show_assigns,
    show_bipartite,
    show_maximal_matching,
    show_min_vertex_cover,
)

Define operator

chose favorite Hamiltonian operator.

1-D Ising model

[2]:

Ising = SumOfProducts([])
J = sympy.Symbol("J")
h = sympy.Symbol("h")
ndim = 5
spin_ops = [OpSite(r"\hat{s}" + f"_{i}", i) for i in range(ndim)]
for i in range(ndim - 1):
    Ising += -J * spin_ops[i] * spin_ops[i + 1]
    Ising -= h * spin_ops[i]
Ising += -h * spin_ops[-1]
Ising = Ising.simplify()
print(f"{Ising.ndim=}, {Ising.nops=}")
Ising.symbol

Ising.ndim=5, Ising.nops=9

[2]:

$\displaystyle - J \hat{s}_0 \hat{s}_1 - J \hat{s}_1 \hat{s}_2 - J \hat{s}_2 \hat{s}_3 - J \hat{s}_3 \hat{s}_4 - h \hat{s}_0 - h \hat{s}_1 - h \hat{s}_2 - h \hat{s}_3 - h \hat{s}_4$

[3]:

Hamiltonian = Ising

Initialze list of assignment information

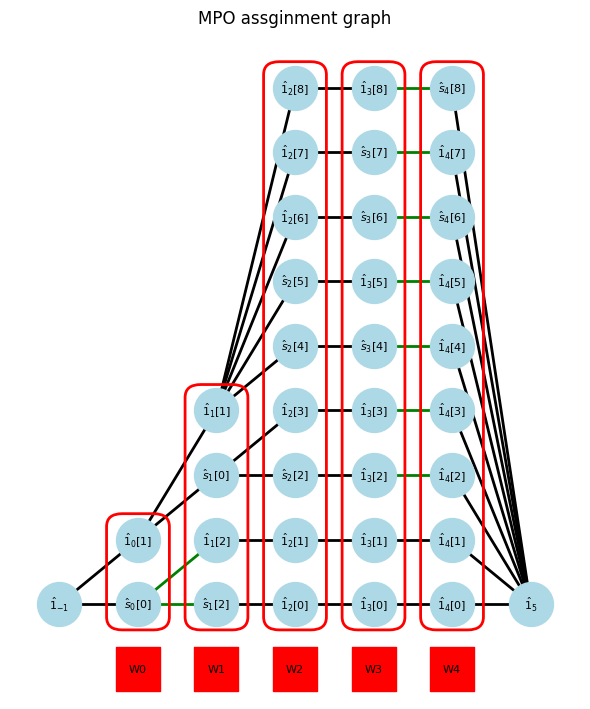
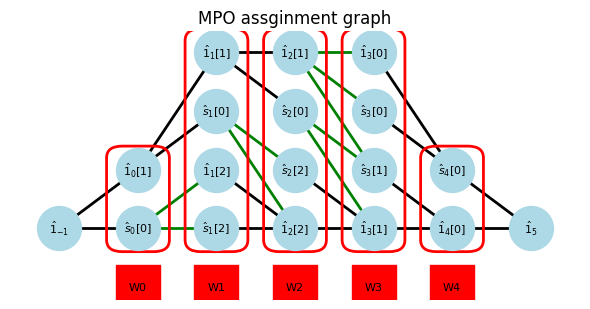
W_assigns holds which row and column each operator is assigned to on each site.
coef_site holds which site coefficient is multiplied to operator.
W is a generated MPO.

[4]:

W_assigns: list[list[int]] = [
    [k for _ in range(Hamiltonian.ndim)] for k in range(Hamiltonian.nops)
]
coef_site: list[int] = [Hamiltonian.ndim - 1 for _ in range(Hamiltonian.nops)]
W: list[sympy.Basic] = []

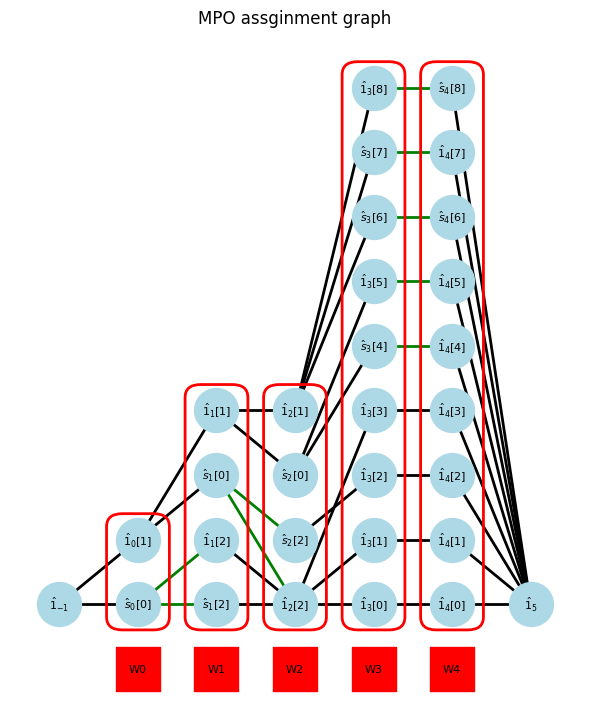
n sum-of-product terms can be naively converted to a MPO with bond dimension M=n. The green edges indicate the mulitplication of the coefficient to the operator.

[5]:

show_assigns(Hamiltonian, W_assigns, coef_site)

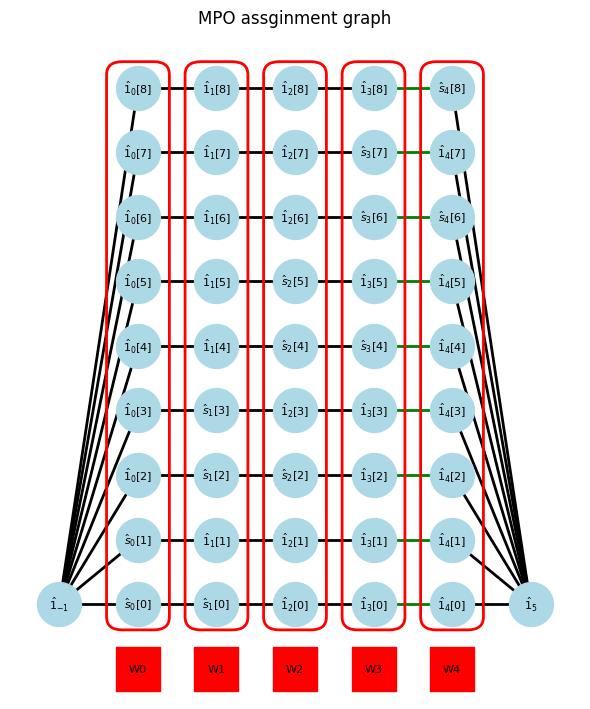
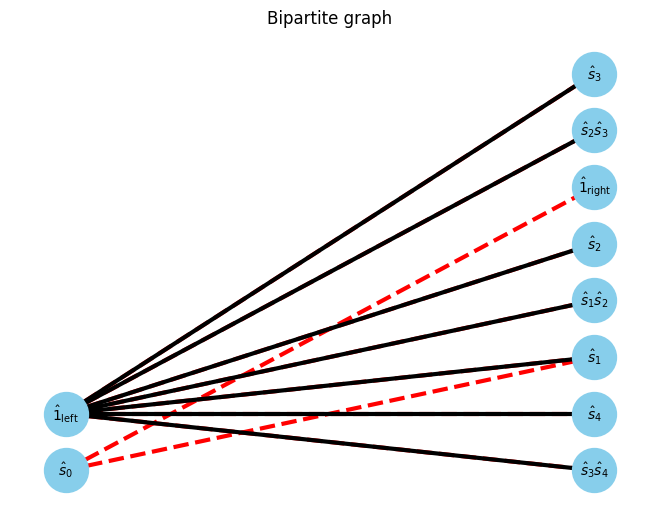
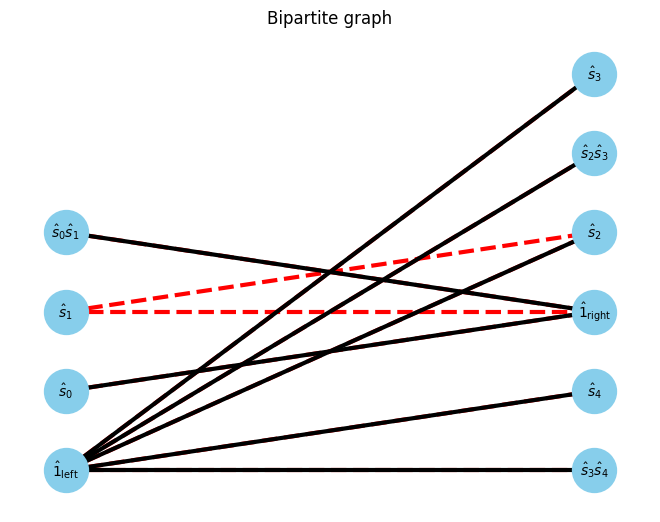
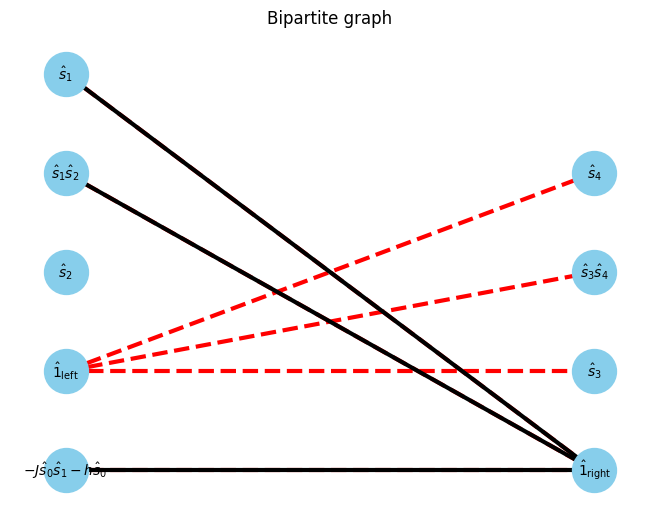
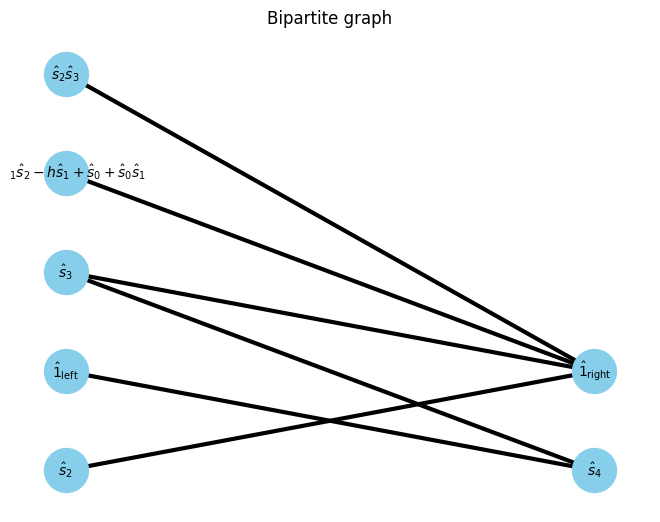
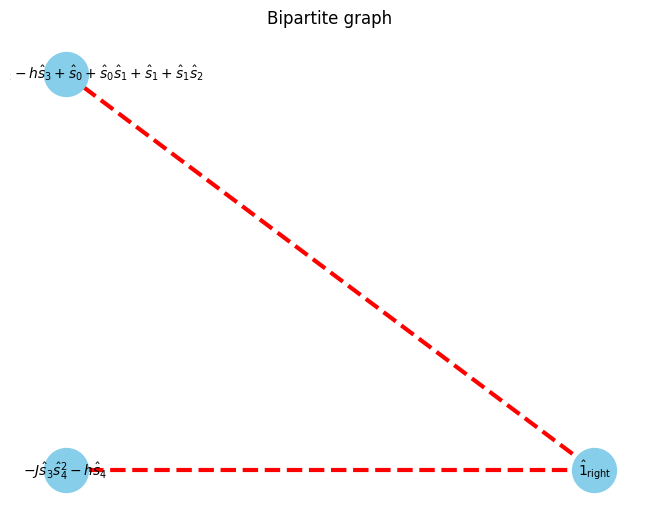
At first, we focus on the gap between 0th and 1st site. The opearator in left blocks and right blocks can be interpreted as a bipartite graph.

[6]:

U, V, E, E_assigns = get_UVE(Hamiltonian, W_assigns, 0)
G, pos = show_bipartite(U, V, E)

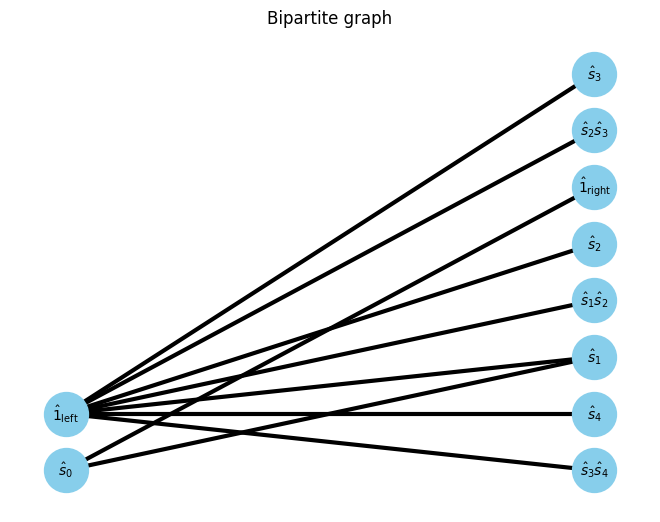
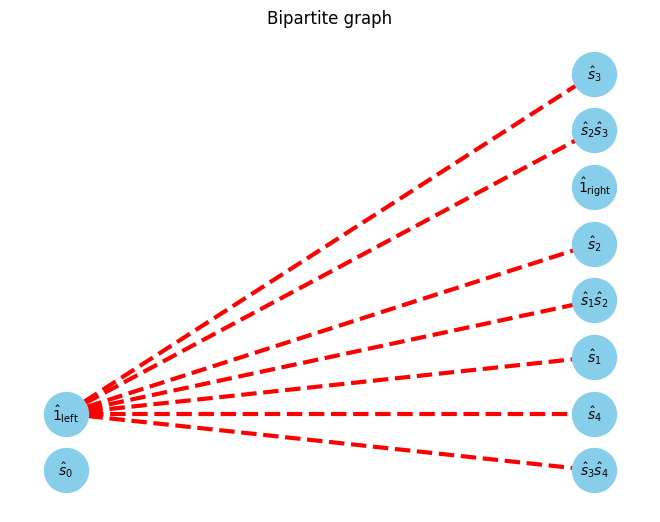
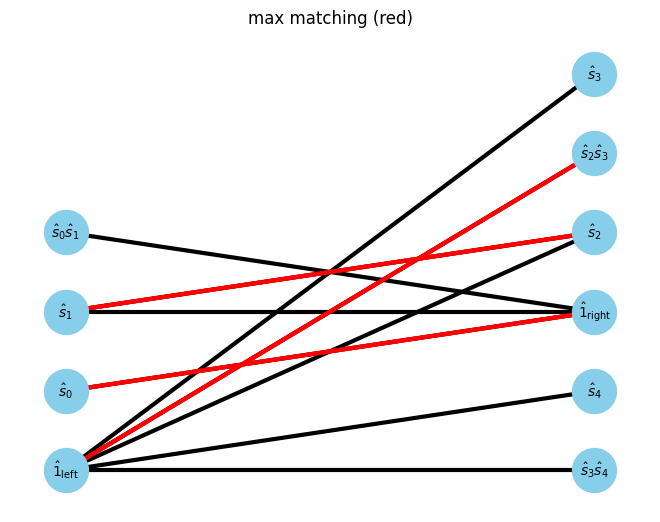
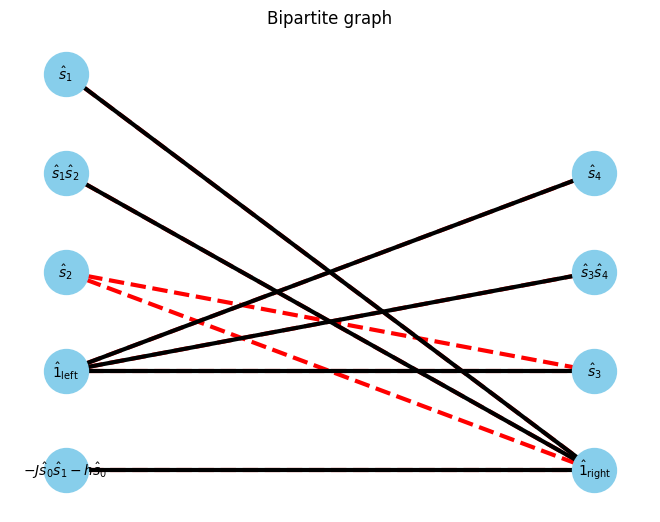
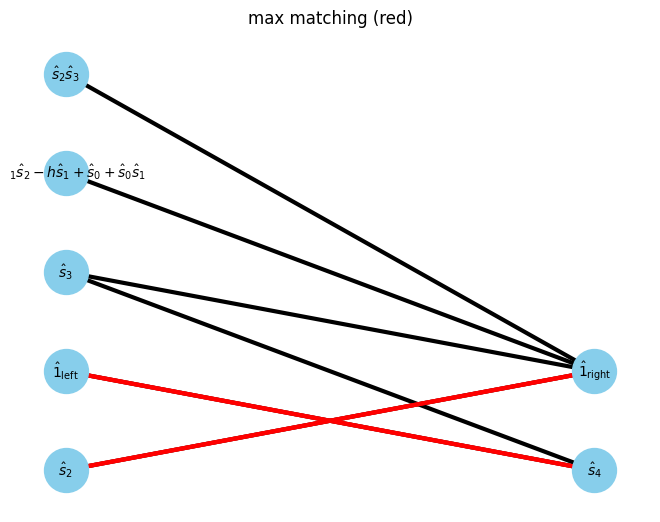
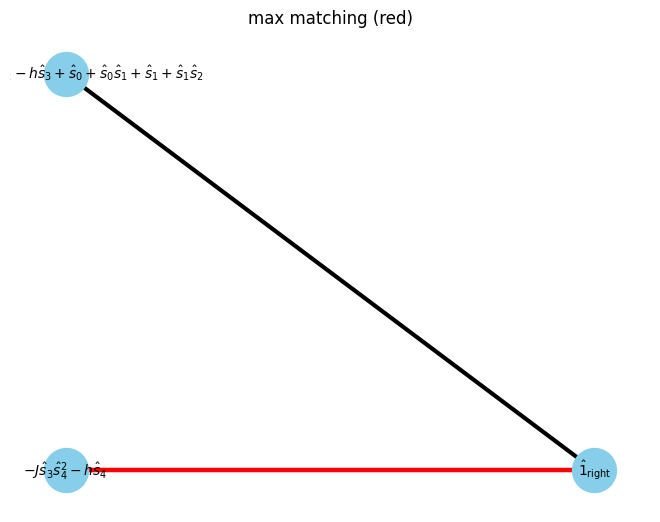
Then, find maxmatching of the bipartite graph

[7]:

max_matching = show_maximal_matching(G, pos)

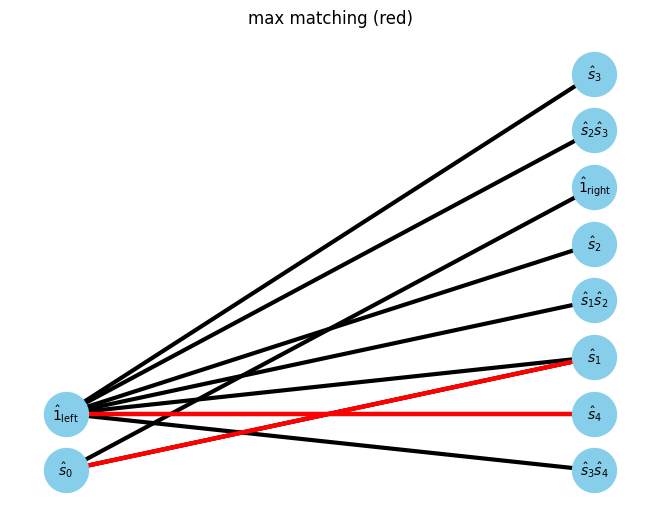
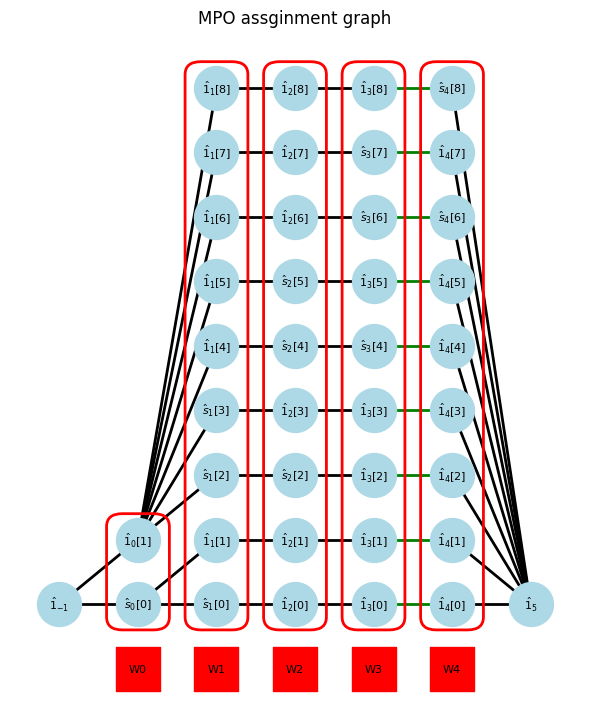
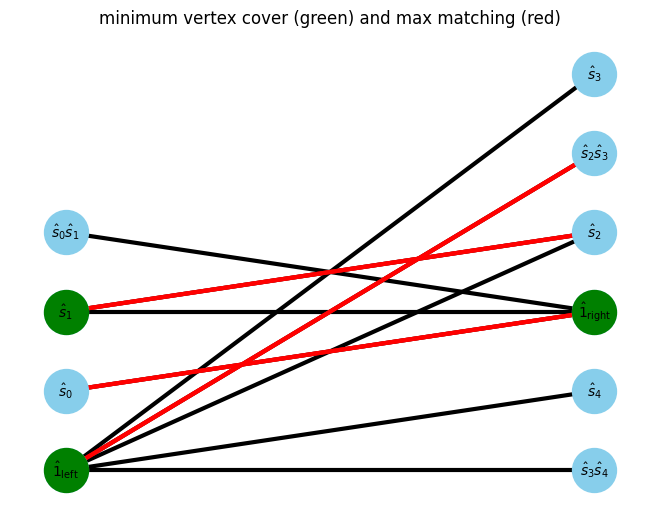
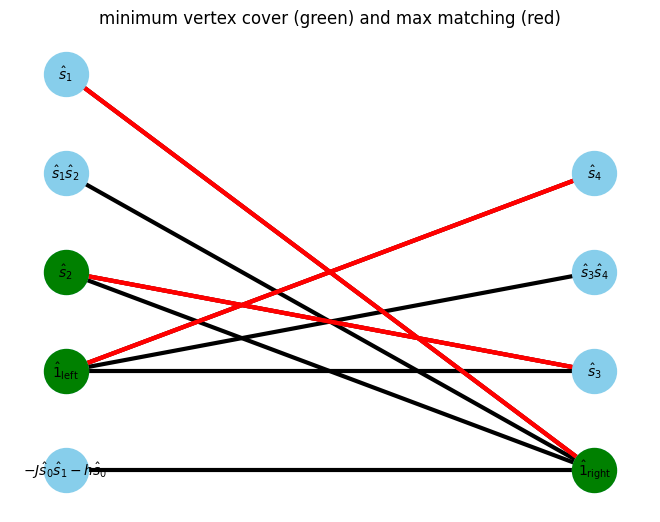
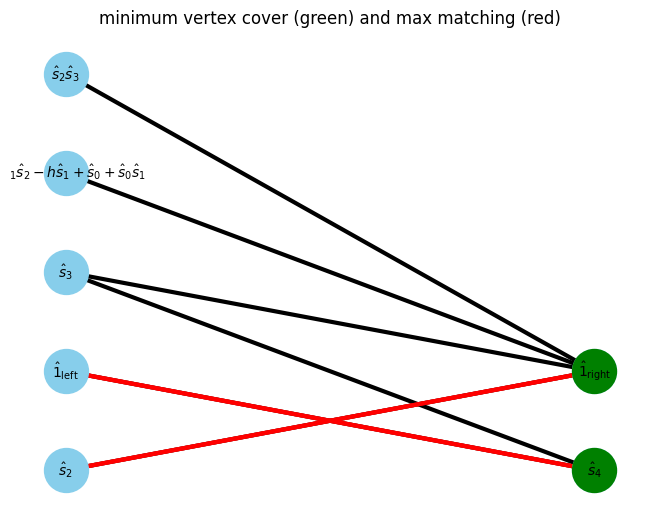
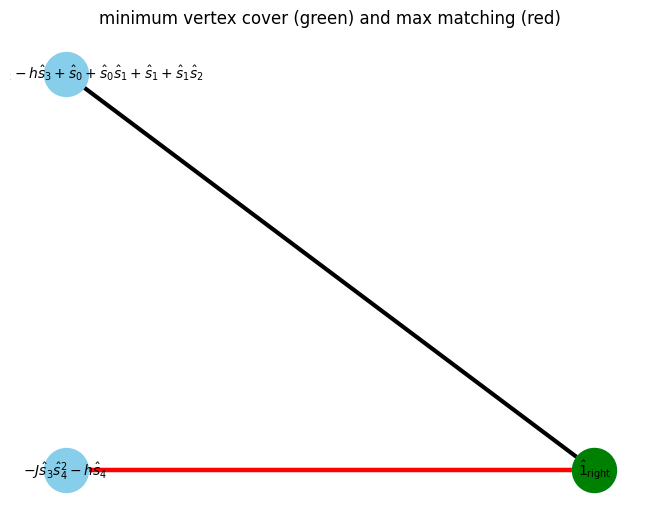
In bipartite graph, the minimum vertex cover (green vertex) can be found from the previous maxmatching.

[8]:

min_vertex_cover = show_min_vertex_cover(G, pos, max_matching)

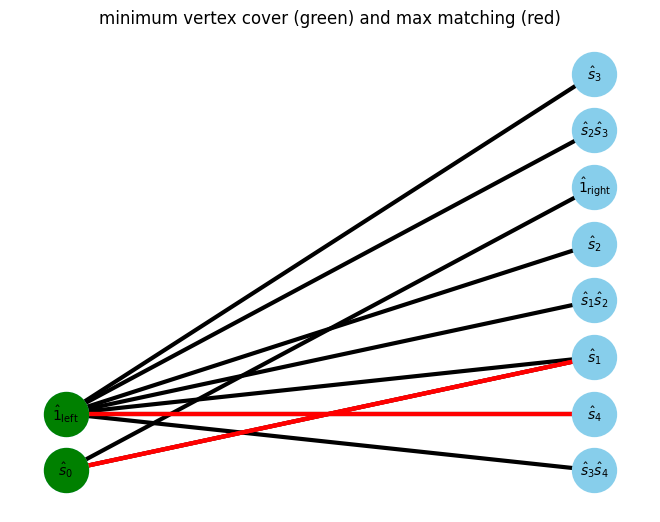
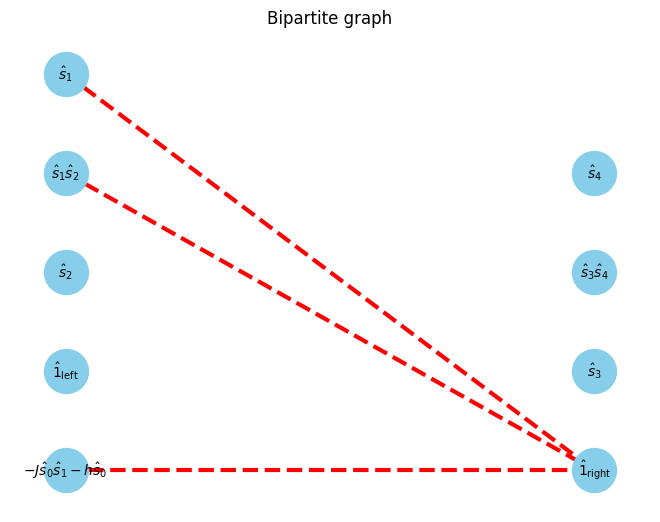
For each minimum vertex covers,

if the vertex cover is in the left side, we can extract normal site operator.
if the vertex cover is in the right side, we can define the complementary operator connected to the vertex cover.

And then, we can assign normal and complementary operators to MPO.

[9]:

Unew, Wi = assign_core(
    min_vertex_cover=min_vertex_cover,
    U=U,
    V=V,
    E=E,
    operators=Hamiltonian,
    isite=0,
    W_assigns=W_assigns,
    E_assigns=E_assigns,
    coef_site=coef_site,
    visualize=True,
)

[10]:

W.append(Wi)
display(*W)

$\displaystyle \left[\begin{matrix}\hat{s}_0 & 1\end{matrix}\right]$

Repeat the same procedure till the end of the MPO.

[11]:

assign_core??

Signature:
assign_core(
    *,
    min_vertex_cover: list[str],
    U: list[str],
    V: list[str],
    E: list[tuple[str, str]],
    operators: pympo.operators.SumOfProducts,
    isite: int,
    W_assigns: list[list[int]],
    E_assigns: list[tuple[str, str]],
    coef_site: list[int],
    visualize: bool = True,
) -> tuple[list[str], sympy.matrices.dense.MutableDenseMatrix]
Source:
def assign_core(
    *,
    min_vertex_cover: list[str],
    U: list[str],
    V: list[str],
    E: list[tuple[str, str]],
    operators: SumOfProducts,
    isite: int,
    W_assigns: list[list[int]],
    E_assigns: list[tuple[str, str]],
    coef_site: list[int],
    visualize: bool = True,
) -> tuple[list[str], sympy.Matrix]:
    """
    Assigns core vertices and updates the bipartite graph representation.
    Parameters:
    -----------
    min_vertex_cover : list[str]
        The minimum vertex cover of the bipartite graph.
    U : list[str]
        List of vertices in set U.
    V : list[str]
        List of vertices in set V.
    E : list[tuple[str, str]]
        List of edges in the bipartite graph.
    operators : SumOfProducts
        The operators to be assigned.
    isite : int
        The current site index.
    W_assigns : list[list[int]]
        The assignments of W.
    E_assigns : list[tuple[str, str]]
        The assignments of edges.
    coef_site : list[int]
        The coefficient sites.
    visualize : bool, optional
        Whether to visualize the bipartite graph and assignments (default is True).
    Returns:
    --------
    tuple[list[str], sympy.Matrix]
        A tuple containing the updated list of vertices in U and the matrix Wi.
    """
    Unew: list[str] = []  # U[1..i]
    unique_ops = []
    update_coef_ops = []
    for j, vertex in enumerate(min_vertex_cover):
        if vertex in U:
            Unew.append(vertex)
            # remove the edge connected to the vertex
            retained_E = []
            remove_E = []
            for edge in E:
                if vertex != edge[0]:
                    retained_E.append(edge)
                else:
                    remove_E.append(edge)
            represent_ops = {}
            for k, op in enumerate(operators.ops):
                if E_assigns[k] in remove_E:
                    opsite = op[isite]
                    W_assigns[k][isite] = j
                    if opsite not in represent_ops:
                        unique_ops.append(k)
                        represent_ops[opsite] = k
        else:
            assert vertex in V, f"{vertex=} is not in {V=}"
            retained_E = []
            remove_E = []
            vertex_U_concat = 0
            for edge in E:
                if vertex != edge[1]:
                    retained_E.append(edge)
                else:
                    remove_E.append(edge)
            represent_ops = {}
            for k, op in enumerate(operators.ops):
                if E_assigns[k] in remove_E:
                    W_assigns[k][isite] = j
                    opsite = op[isite]
                    if coef_site[k] >= isite:
                        unique_ops.append(k)
                    elif opsite not in represent_ops:
                        unique_ops.append(k)
                        represent_ops[opsite] = k

                    op_0_to_isite = op[0 : isite + 1]
                    if coef_site[k] < isite:
                        vertex_U_concat += op_0_to_isite
                    else:
                        # coef_site[k] = isite
                        update_coef_ops.append(k)
                        vertex_U_concat += op.coef * op_0_to_isite
            Unew.append(sympy.srepr(vertex_U_concat))
        if visualize:
            pympo.visualize.show_bipartite(U, V, E, retained_E)
        E = retained_E
    for k in update_coef_ops:
        coef_site[k] = isite
    if visualize:
        pympo.visualize.show_assigns(operators, W_assigns, coef_site)
    if isite == 0:
        left_dim = 1
    else:
        left_dim = max([assign[isite - 1] for assign in W_assigns]) + 1
    if isite == operators.ndim - 1:
        right_dim = 1
    else:
        right_dim = len(Unew)
        right_dim_debug = max([assign[isite] for assign in W_assigns]) + 1
        assert (
            right_dim == right_dim_debug
        ), f"{right_dim} != {right_dim_debug}, {[assign[isite] for assign in W_assigns]}"
    Wi = sympy.zeros(left_dim, right_dim)
    for k in unique_ops:
        op = operators.ops[k]
        if isite == 0:
            left_index = 0
        else:
            left_index = W_assigns[k][isite - 1]
        if isite == operators.ndim - 1:
            right_index = 0
        else:
            right_index = W_assigns[k][isite]
        if sympy.latex(op[isite]) == r"\hat{1}" + f"_{isite}":
            opisite = 1
        else:
            opisite = op[isite]
        # there are three cases
        # 1. W[a,b] = x_i
        # 2. W[a,b] += x_i
        # 3. W[a,b] += coef * x_i
        if coef_site[k] == isite:
            # case 3
            Wi[left_index, right_index] += op.coef * opisite
        elif coef_site[k] < isite:
            Wi[left_index, right_index] += opisite
        else:
            # case 1
            if Wi[left_index, right_index] == 0:
                Wi[left_index, right_index] = opisite
            else:
                assert (
                    Wi[left_index, right_index] == opisite
                ), f"{Wi[left_index, right_index]=} while {op[isite]=} when {coef_site[k]=}, {isite=}"
    return Unew, Wi
File:      ~/GitHub/PyMPO/src/pympo/bipartite.py
Type:      function

[12]:

for isite in range(1, Hamiltonian.ndim):
    print(f"{isite=}")
    U, V, E, E_assigns = get_UVE(Hamiltonian, W_assigns, isite, Unew)
    G, pos = show_bipartite(U, V, E)
    max_matching = show_maximal_matching(G, pos)
    min_vertex_cover = show_min_vertex_cover(G, pos, max_matching)
    Unew, Wi = assign_core(
        min_vertex_cover=min_vertex_cover,
        U=U,
        V=V,
        E=E,
        operators=Hamiltonian,
        isite=isite,
        W_assigns=W_assigns,
        E_assigns=E_assigns,
        coef_site=coef_site,
        visualize=True,
    )
    W.append(Wi)
    display(*W)
    W_prod = sympy.Mul(*W)
    print(*[f"W{i}" for i in range(isite + 1)], "=")
    display(W_prod.expand())

isite=1

$\displaystyle \left[\begin{matrix}\hat{s}_0 & 1\end{matrix}\right]$

$\displaystyle \left[\begin{matrix}0 & 0 & - J \hat{s}_1 - h\\\hat{s}_1 & 1 & 0\end{matrix}\right]$

W0 W1 =

$\displaystyle \left[\begin{matrix}\hat{s}_1 & 1 & - J \hat{s}_0 \hat{s}_1 - h \hat{s}_0\end{matrix}\right]$

isite=2

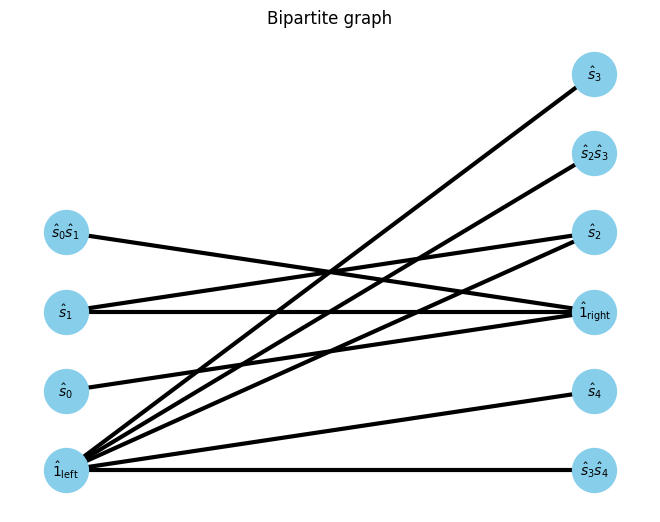
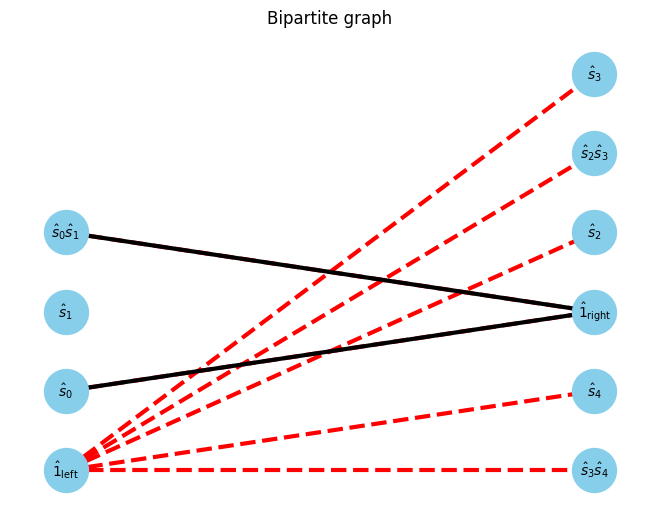
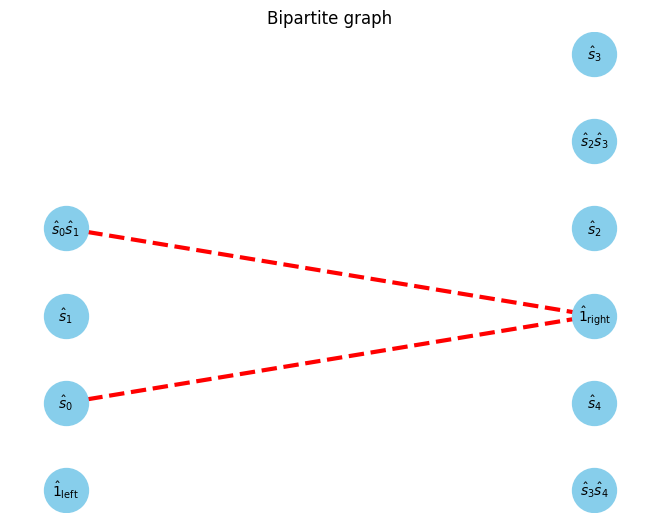
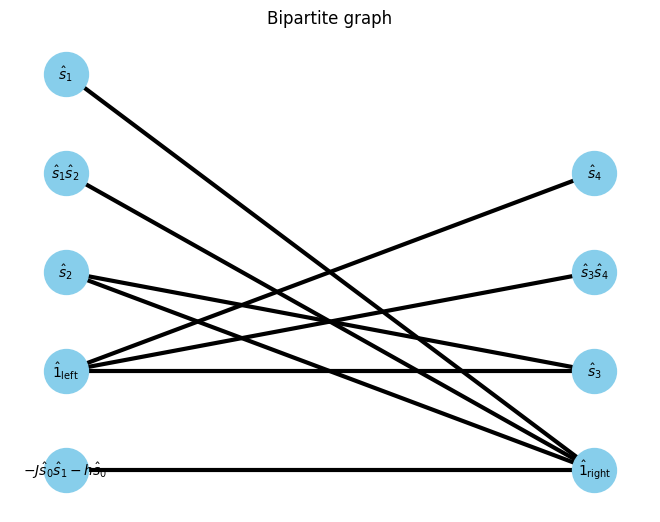
../_images/example_autompo-sym_21_13.png

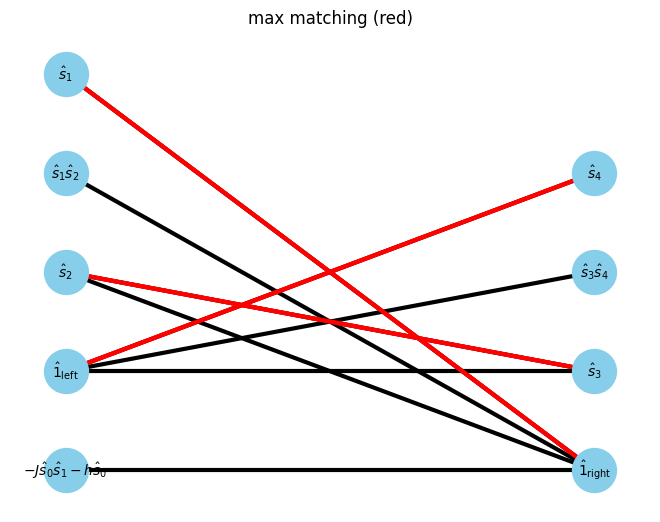
../_images/example_autompo-sym_21_14.png

../_images/example_autompo-sym_21_15.png

../_images/example_autompo-sym_21_16.png

../_images/example_autompo-sym_21_17.png

../_images/example_autompo-sym_21_18.png

../_images/example_autompo-sym_21_19.png

$\displaystyle \left[\begin{matrix}\hat{s}_0 & 1\end{matrix}\right]$

$\displaystyle \left[\begin{matrix}0 & 0 & - J \hat{s}_1 - h\\\hat{s}_1 & 1 & 0\end{matrix}\right]$

$\displaystyle \left[\begin{matrix}0 & 0 & - J \hat{s}_2 - h\\\hat{s}_2 & 1 & 0\\0 & 0 & 1\end{matrix}\right]$

W0 W1 W2 =

$\displaystyle \left[\begin{matrix}\hat{s}_2 & 1 & - J \hat{s}_0 \hat{s}_1 - J \hat{s}_1 \hat{s}_2 - h \hat{s}_0 - h \hat{s}_1\end{matrix}\right]$

isite=3

../_images/example_autompo-sym_21_26.png

../_images/example_autompo-sym_21_27.png

../_images/example_autompo-sym_21_28.png

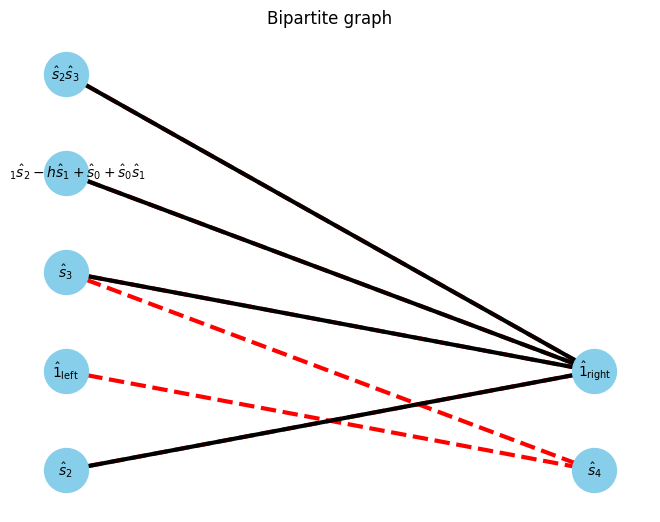
../_images/example_autompo-sym_21_29.png

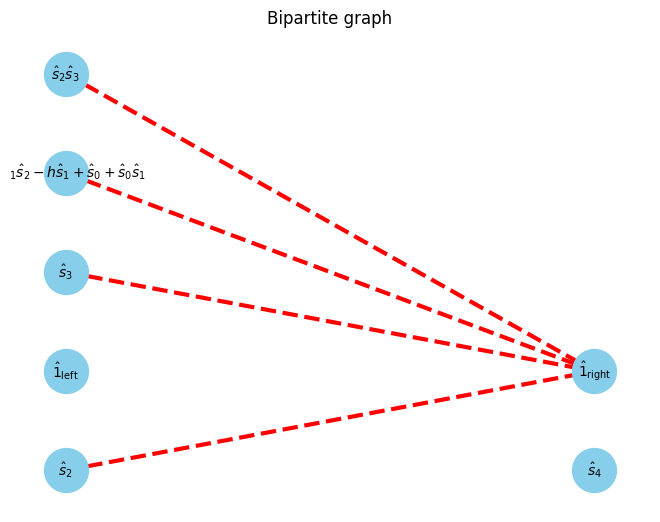
../_images/example_autompo-sym_21_30.png

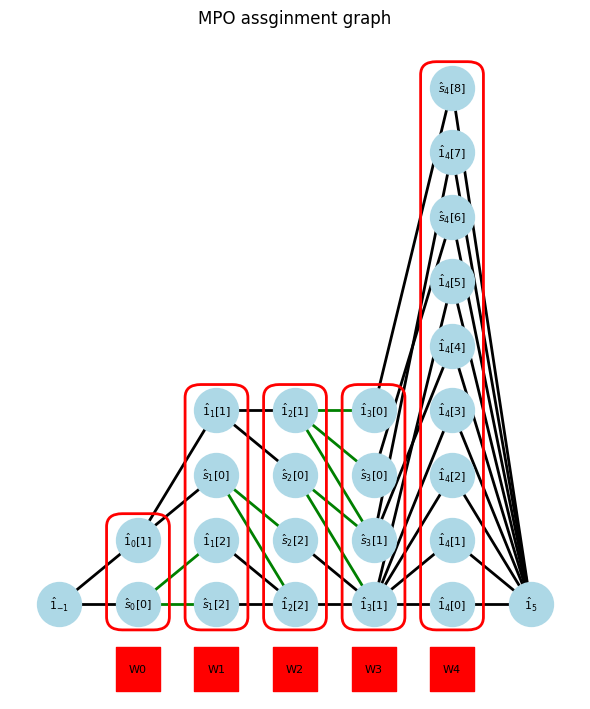
../_images/example_autompo-sym_21_31.png

$\displaystyle \left[\begin{matrix}\hat{s}_0 & 1\end{matrix}\right]$

$\displaystyle \left[\begin{matrix}0 & 0 & - J \hat{s}_1 - h\\\hat{s}_1 & 1 & 0\end{matrix}\right]$

$\displaystyle \left[\begin{matrix}0 & 0 & - J \hat{s}_2 - h\\\hat{s}_2 & 1 & 0\\0 & 0 & 1\end{matrix}\right]$

$\displaystyle \left[\begin{matrix}0 & - J \hat{s}_3 - h\\- J \hat{s}_3 - h & - h \hat{s}_3\\0 & 1\end{matrix}\right]$

W0 W1 W2 W3 =

$\displaystyle \left[\begin{matrix}- J \hat{s}_3 - h & - J \hat{s}_0 \hat{s}_1 - J \hat{s}_1 \hat{s}_2 - J \hat{s}_2 \hat{s}_3 - h \hat{s}_0 - h \hat{s}_1 - h \hat{s}_2 - h \hat{s}_3\end{matrix}\right]$

isite=4

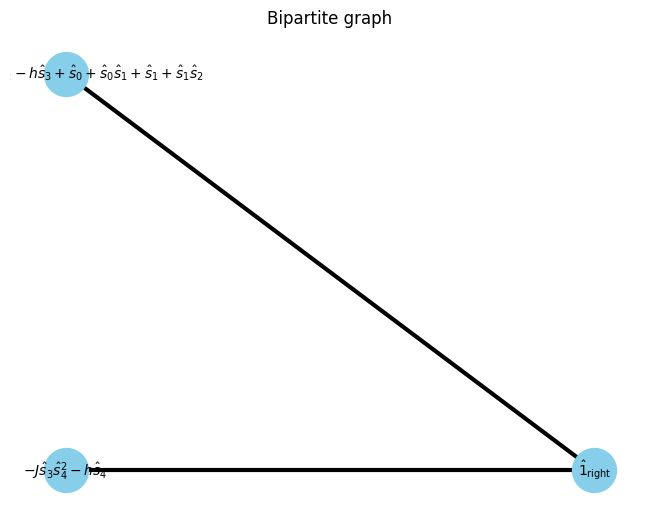
../_images/example_autompo-sym_21_39.png

../_images/example_autompo-sym_21_40.png

../_images/example_autompo-sym_21_41.png

../_images/example_autompo-sym_21_42.png

../_images/example_autompo-sym_21_43.png

$\displaystyle \left[\begin{matrix}\hat{s}_0 & 1\end{matrix}\right]$

$\displaystyle \left[\begin{matrix}0 & 0 & - J \hat{s}_1 - h\\\hat{s}_1 & 1 & 0\end{matrix}\right]$

$\displaystyle \left[\begin{matrix}0 & 0 & - J \hat{s}_2 - h\\\hat{s}_2 & 1 & 0\\0 & 0 & 1\end{matrix}\right]$

$\displaystyle \left[\begin{matrix}0 & - J \hat{s}_3 - h\\- J \hat{s}_3 - h & - h \hat{s}_3\\0 & 1\end{matrix}\right]$

$\displaystyle \left[\begin{matrix}\hat{s}_4\\1\end{matrix}\right]$

W0 W1 W2 W3 W4 =

$\displaystyle \left[\begin{matrix}- J \hat{s}_0 \hat{s}_1 - J \hat{s}_1 \hat{s}_2 - J \hat{s}_2 \hat{s}_3 - J \hat{s}_3 \hat{s}_4 - h \hat{s}_0 - h \hat{s}_1 - h \hat{s}_2 - h \hat{s}_3 - h \hat{s}_4\end{matrix}\right]$