Custom neural network combined with tensor train

Let’s hacking Pompon!

One will use tensor train implementaion in Pompon and customized neural network build by Flax

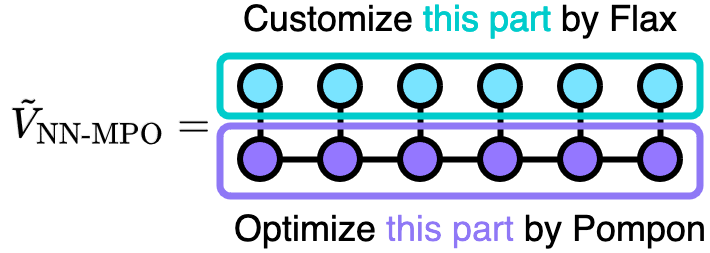
Before start, install Flax. In this example, we will follow flax.nnx API rather than flax.linen API.

try:
    from flax import nnx
except ModuleNotFoundError:
    !uv pip install --quiet flax

Import modules

import jax
import jax.numpy as jnp
import matplotlib.pyplot as plt
import numpy as np
import optax
from tqdm.auto import tqdm

from pompon import DTYPE
from pompon._jittables import _forward_basis2y
from pompon.layers.tt import TensorTrain
from pompon.optimizer.sweeper import sweep

Prepare training data

We will use \[ y = \boldsymbol{x}A\boldsymbol{x}^\top \] as a true function

def generate_data(num_samples, key, include_f=True):
    mean = jnp.zeros(3)
    cov = jnp.eye(3)
    k = 1.0

    A = k * jnp.linalg.inv(cov)

    x_samples = jax.random.multivariate_normal(
        key=key, mean=mean, cov=cov, shape=(num_samples,), dtype=DTYPE
    )
    y_samples = jnp.einsum("ni,ij,nj->n", x_samples, A, x_samples)

    if include_f:
        f_samples = -2.0 * x_samples @ A
        return x_samples, y_samples[:, jnp.newaxis], f_samples
    else:
        return x_samples, y_samples[:, jnp.newaxis]


num_samples = 256
key = jax.random.PRNGKey(0)
x_samples, y_samples, f_samples = generate_data(num_samples, key)

print("x samples:", x_samples.shape, x_samples.dtype)
print("y samples:", y_samples.shape, y_samples.dtype)
print("f samples:", f_samples.shape, f_samples.dtype)

x samples: (256, 3) float64
y samples: (256, 1) float64
f samples: (256, 3) float64

Define Custom Network

Define Basis function

Define network like this;

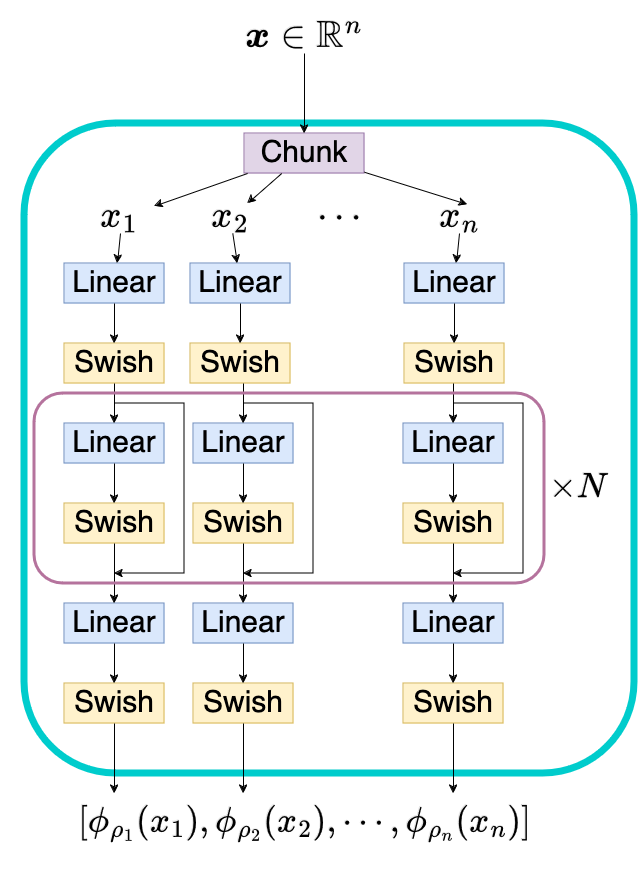
where \(\phi_{\rho_i}(x_i): \mathbb{R}\to\mathbb{R}^d\) and \(d\) is a number of basis (chunk_size).

class CustomBasis(nnx.Module):
    """
    Args:
        num_chunks (int): degree of freedoms n
        hidden_size (int): hidden layer size
        chunk_size (int): number of basis for each mode
        n_layers (int): number of hidden layers
        rngs (nnx.Rngs): random generator

    """

    def __init__(
        self,
        num_chunks: int,
        hidden_size: int,
        chunk_size: int,
        n_layers: int,
        x_scale: jax.Array,
        rngs: nnx.Rngs,
    ):
        self.num_chunks = num_chunks
        self.hidden_size = hidden_size
        self.chunk_size = chunk_size
        self.n_layers = n_layers
        self.x_scale = x_scale
        initializer = jax.nn.initializers.glorot_uniform()
        self.w_ini = nnx.Param(
            initializer(
                rngs.params(),
                (self.num_chunks, self.hidden_size),
                dtype=DTYPE,
            )
        )
        self.b_ini = nnx.Param(
            jnp.zeros((self.num_chunks, self.hidden_size), dtype=DTYPE)
        )

        self.w_mid = []
        self.b_mid = []
        for _ in range(n_layers):
            self.w_mid.append(
                nnx.Param(
                    initializer(
                        rngs.params(),
                        (self.hidden_size, self.hidden_size),
                        dtype=DTYPE,
                    )
                )
            )
            self.b_mid.append(
                nnx.Param(
                    jnp.zeros((self.num_chunks, self.hidden_size), dtype=DTYPE)
                )
            )
        self.w_fin = nnx.Param(
            initializer(
                rngs.params(),
                (self.hidden_size, self.chunk_size),
                dtype=DTYPE,
            )
        )
        self.b_fin = nnx.Param(
            jnp.zeros((self.num_chunks, self.chunk_size), dtype=DTYPE)
        )

    def __call__(self, x: jax.Array, i: int | None = None) -> list[jax.Array]:
        r"""
        Args:
            x (jax.Array): input position with shape (batch_size, DOFs)
            i (int, optional): If you need only i-th basis $\phi_{\rho_i}$, 
                set this integer.

        Returns:
            list[jax.Array]: list of $\phi_{\rho_i}$ with length `num_chunks`.
                Each basis has shape `(chunk_size,)`.
        """

        if i is None:
            index: slice = slice(0, x.shape[1])
        else:
            index: slice = slice(i, i + 1)
            if x.ndim == 1:
                x = x[:, jnp.newaxis]  # batch, 1
            elif x.ndim == 2:
                assert x.shape[1] == 1
            else:
                raise ValueError(f"{x.ndim=} is invalid")
        ndim = x.shape[1]

        x = x / self.x_scale[jnp.newaxis, index]
        x = (
            self.w_ini[jnp.newaxis, index, :] * x[:, :, jnp.newaxis]
        )  # batch, num_chunks, hidden_size
        x = x + self.b_ini[jnp.newaxis, index, :]
        x = nnx.swish(x)

        for i in range(self.n_layers):
            res = x
            x = x @ self.w_mid[i]  # batch, num_chunks, hidden_size
            x = x + self.b_mid[i][jnp.newaxis, index, :]
            x = nnx.swish(x) + res

        x = x @ self.w_fin  # batch, num_chunks, chunk_size
        x = x + self.b_fin[jnp.newaxis, index, :]
        x = nnx.swish(x)

        phi_chunked_array = jnp.split(x, ndim, axis=1)
        phi_chunked_list = [item.squeeze(1) for item in phi_chunked_array]

        return phi_chunked_list

x = jnp.arange(3 * 2).reshape(2, 3)

basis = CustomBasis(
    num_chunks=3, hidden_size=4, chunk_size=2, n_layers=3, x_scale=x.std(axis=0),rngs=nnx.Rngs(0)
)
print(basis(x=x))
print(basis(x=x[:, 0:1], i=0))

[Array([[ 0.        ,  0.        ],
       [-0.27816969, -0.27609677]], dtype=float64), Array([[0.16544799, 0.16702912],
       [0.47790957, 0.3542889 ]], dtype=float64), Array([[ 0.67407335,  0.36907104],
       [ 0.45613932, -0.21072378]], dtype=float64)]
[Array([[ 0.        ,  0.        ],
       [-0.27816969, -0.27609677]], dtype=float64)]

Define Custom Model including the Custom Basis

class CustomModel(nnx.Module):
    """
    Args:
        num_chunks (int): degree of freedoms n
        hidden_size (int): hidden layer size
        chunk_size (int): number of basis for each mode
        n_layers (int): number of hidden layers
        rngs (nnx.Rngs): random generator

    """

    def __init__(
        self,
        num_chunks: int,
        hidden_size: int,
        chunk_size: int,
        n_layers: int,
        x_scale: jax.Array,
        rngs: nnx.Rngs,
    ):
        self.num_chunks = num_chunks
        self.hidden_size = hidden_size
        self.chunk_size = chunk_size
        self.n_layers = n_layers

        self.basis = CustomBasis(
            num_chunks=self.num_chunks,
            hidden_size=self.hidden_size,
            chunk_size=self.chunk_size,
            n_layers=self.n_layers,
            x_scale=x_scale,
            rngs=rngs,
        )

    def __call__(self, x: jax.Array, W: list[jax.Array], norm: jax.Array):
        """
        Args:
            x (jax.Array): input position with shape (batch_size, DOFs)
            W (list[jax.Array]): list of tensor train core. 
                Each core has shape (bond_dim1, chunk_size, bond_dim2).
            norm (jax.Array): Scalar which scales outputs.
        """
        basis = self.basis(x)
        return _forward_basis2y(basis=basis, W=W, norm=norm)


model = CustomModel(
    num_chunks=3, hidden_size=16, chunk_size=2, n_layers=16, x_scale=x_samples.std(axis=0), rngs=nnx.Rngs(0)
)
nnx.display(model)

CustomModel(
  num_chunks=3,
  hidden_size=16,
  chunk_size=2,
  n_layers=16,
  basis=CustomBasis(
    num_chunks=3,
    hidden_size=16,
    chunk_size=2,
    n_layers=16,
    x_scale=Array(shape=(3,), dtype=float64),
    w_ini=Param(
      value=Array(shape=(3, 16), dtype=float64)
    ),
    b_ini=Param(
      value=Array(shape=(3, 16), dtype=float64)
    ),
    w_mid=[Param(
      value=Array(shape=(16, 16), dtype=float64)
    ), Param(
      value=Array(shape=(16, 16), dtype=float64)
    ), Param(
      value=Array(shape=(16, 16), dtype=float64)
    ), Param(
      value=Array(shape=(16, 16), dtype=float64)
    ), Param(
      value=Array(shape=(16, 16), dtype=float64)
    ), Param(
      value=Array(shape=(16, 16), dtype=float64)
    ), Param(
      value=Array(shape=(16, 16), dtype=float64)
    ), Param(
      value=Array(shape=(16, 16), dtype=float64)
    ), Param(
      value=Array(shape=(16, 16), dtype=float64)
    ), Param(
      value=Array(shape=(16, 16), dtype=float64)
    ), Param(
      value=Array(shape=(16, 16), dtype=float64)
    ), Param(
      value=Array(shape=(16, 16), dtype=float64)
    ), Param(
      value=Array(shape=(16, 16), dtype=float64)
    ), Param(
      value=Array(shape=(16, 16), dtype=float64)
    ), Param(
      value=Array(shape=(16, 16), dtype=float64)
    ), Param(
      value=Array(shape=(16, 16), dtype=float64)
    )],
    b_mid=[Param(
      value=Array(shape=(3, 16), dtype=float64)
    ), Param(
      value=Array(shape=(3, 16), dtype=float64)
    ), Param(
      value=Array(shape=(3, 16), dtype=float64)
    ), Param(
      value=Array(shape=(3, 16), dtype=float64)
    ), Param(
      value=Array(shape=(3, 16), dtype=float64)
    ), Param(
      value=Array(shape=(3, 16), dtype=float64)
    ), Param(
      value=Array(shape=(3, 16), dtype=float64)
    ), Param(
      value=Array(shape=(3, 16), dtype=float64)
    ), Param(
      value=Array(shape=(3, 16), dtype=float64)
    ), Param(
      value=Array(shape=(3, 16), dtype=float64)
    ), Param(
      value=Array(shape=(3, 16), dtype=float64)
    ), Param(
      value=Array(shape=(3, 16), dtype=float64)
    ), Param(
      value=Array(shape=(3, 16), dtype=float64)
    ), Param(
      value=Array(shape=(3, 16), dtype=float64)
    ), Param(
      value=Array(shape=(3, 16), dtype=float64)
    ), Param(
      value=Array(shape=(3, 16), dtype=float64)
    )],
    w_fin=Param(
      value=Array(shape=(16, 2), dtype=float64)
    ),
    b_fin=Param(
      value=Array(shape=(3, 2), dtype=float64)
    )
  )
)

Extract required arguments from TensorTrain modules

def get_norm_W(tt: TensorTrain) -> tuple[jax.Array, list[jax.Array]]:
    """
    Get norm & tt-cores.
    """
    W = [getattr(tt, f"W{i}").data for i in range(len(tt))]
    norm = tt.norm.data
    return norm, W

Initialize tensor train.

See also pompon.layers.tt.TensorTrain.

tt = TensorTrain.set_random(
    shape=(model.chunk_size,) * model.num_chunks, rank=2
)
norm, W = get_norm_W(tt)
print(norm, W)
x = jnp.array([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
basis = model.basis(x)
print(basis)
y_chunked = model(x, W, norm)
print(y_chunked)

2.738025133756779 [Array([[[ 0.269559  ,  0.48521447],
        [-0.66477019, -0.49998546]]], dtype=float64), Array([[[-2.69638259,  0.02057865],
        [ 6.39613801, -0.46289717]],

       [[-1.33265668, -0.4078536 ],
        [ 5.44471885,  0.45414894]]], dtype=float64), Array([[[-0.47058099],
        [ 0.88235681]],

       [[-0.88235681],
        [-0.47058099]]], dtype=float64)]
[Array([[-1.12089883e-02,  4.54244220e-01],
       [-3.01759052e-47,  4.94457722e+00]], dtype=float64), Array([[-2.47008425e-01, -2.40598015e-01],
       [-2.47244541e-19, -4.38226713e-02]], dtype=float64), Array([[-8.55275875e-18,  5.79409551e-01],
       [-8.68260031e-86, -1.70533086e-02]], dtype=float64)]
[[ 0.71465496]
 [-0.06264489]]

Train with energy

Train basis with fixed tensor-train

@nnx.jit  # <- not jax.jit! because model is not jax.Array
def train_step(model, optimizer, x, y, W, norm):
    def _loss_fn(model):
        pred = model(x, W, norm)
        loss = jnp.mean((pred - y) ** 2)
        return loss

    loss, grads = nnx.value_and_grad(_loss_fn)(model)
    optimizer.update(grads)
    return loss

optimizer = nnx.Optimizer(model, optax.adam(1e-03))
loss = train_step(model, optimizer, x_samples, y_samples, W, norm)

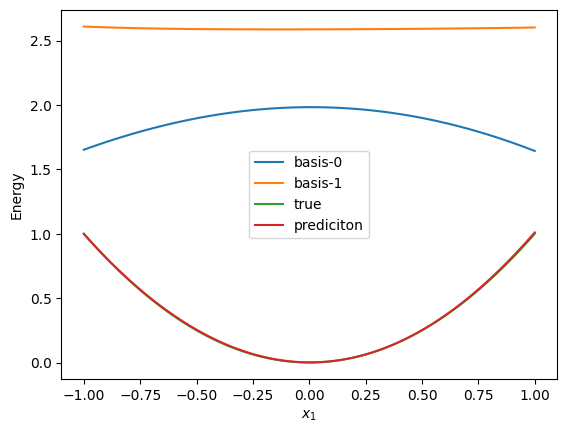
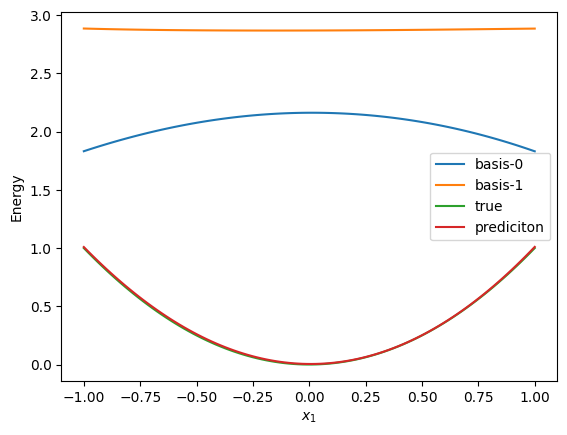
Visualize basis

def show_basis(model, tt):
    x0 = np.linspace(-1, 1, 100)
    x = np.zeros((100, 3))
    x[:, 0] = x0
    basis = model.basis(jnp.array(x))
    for i in range(model.chunk_size):
        plt.plot(x0, np.array(basis[0][:, i]), label=f"basis-{i}")
    plt.plot(x0, x0**2, label="true")
    norm, W = get_norm_W(tt)
    y = model(jnp.array(x), W, norm)
    plt.plot(x0, np.array(y.squeeze(1)), label="prediciton")
    plt.legend()
    plt.xlabel("$x_1$")
    plt.ylabel("Energy")
    plt.show()


show_basis(model, tt)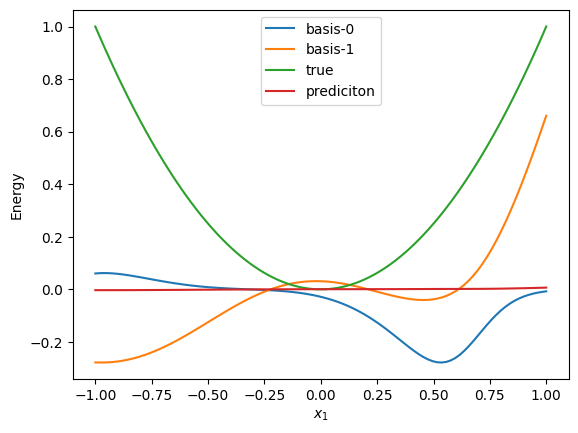

Train basis iteratively

losses = []
norm, W = get_norm_W(tt)
for _ in tqdm(range(1000)):
    loss = train_step(model, optimizer, x_samples, y_samples, W, norm)
    losses.append(loss)

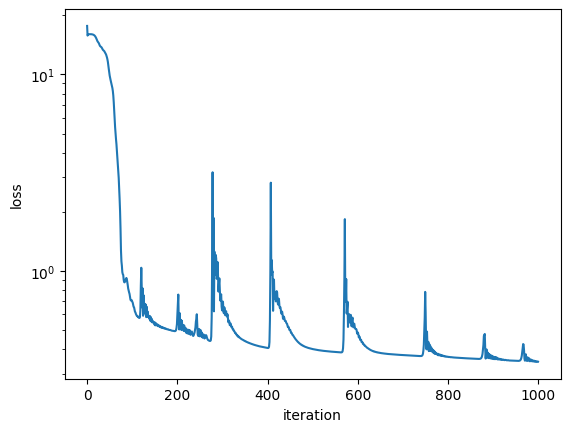
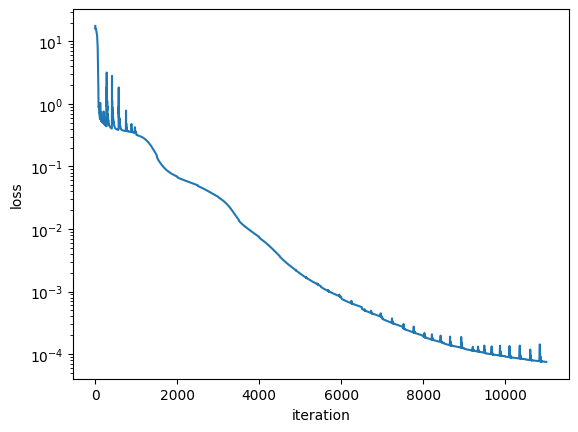
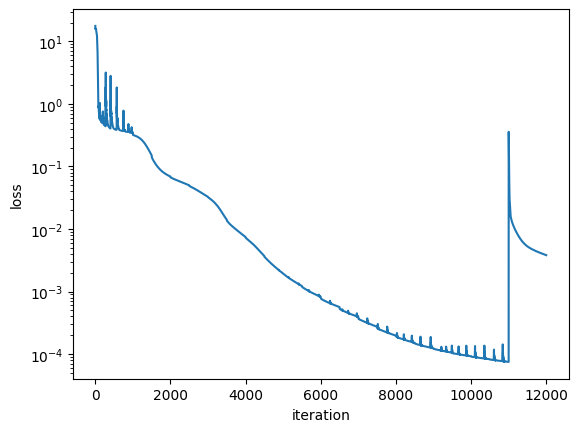
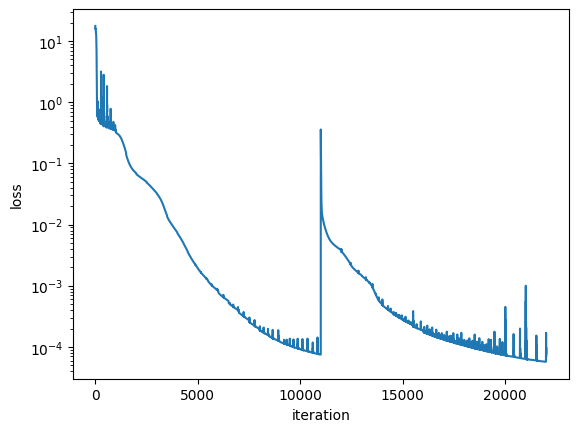
Show training trace

def show_trace(losses):
    plt.plot(losses)
    plt.xlabel("iteration")
    plt.ylabel("loss")
    plt.yscale("log")
    plt.show()


show_trace(losses)

Train tensor train with fixed basis

See also pompon.optimizer.sweeper.sweep.

sweep?

Signature:
sweep(
    *,
    tt: pompon.layers.tt.TensorTrain,
    basis: list[jax.Array],
    y: jax.Array,
    nsweeps: int = 2,
    maxdim: int | list[int] | numpy.ndarray = 30,
    cutoff: float | list[float] | numpy.ndarray = 0.01,
    optax_solver: optax._src.base.GradientTransformation | None = None,
    opt_maxiter: int = 1000,
    opt_tol: float | list[float] | numpy.ndarray | None = None,
    opt_lambda: float = 0.0,
    onedot: bool = False,
    use_CG: bool = False,
    use_scipy: bool = False,
    use_jax_scipy: bool = False,
    method: str = 'L-BFGS-B',
    ord: str = 'fro',
    auto_onedot: bool = True,
)
Docstring:
Tensor-train sweep optimization
Args:
    tt (TensorTrain): the tensor-train model.
    basis (list[Array]): the basis functions.
    y (Array): the target values.
    nsweeps (int): The number of sweeps.
    maxdim (int, list[int]): the maximum rank of TT-sweep.
    cutoff (float, list[float]): the ratio of truncated singular values for TT-sweep.
        When one-dot core is optimized, this parameter is not used.
    optax_solver (optax.GradientTransformation): the optimizer for TT-sweep.
        Defaults to None. If None, the optimizer is not used.
    opt_maxiter (int): the maximum number of iterations for TT-sweep.
    opt_tol (float, list[float]): the convergence criterion of gradient for TT-sweep.
        Defaults to None, i.e., opt_tol = cutoff.
    opt_lambda (float): the L2 regularization parameter for TT-sweep.
        Only use_CG=True is supported.
    onedot (bool, optional): whether to optimize one-dot or two-dot core.
        Defaults to False, i.e. two-dot core optimization.
    use_CG (bool, optional): whether to use conjugate gradient method for TT-sweep.
        Defaults to False. CG is suitable for one-dot core optimization.
    use_scipy (bool, optional): whether to use scipy.optimize.minimize for TT-sweep.
        Defaults to False and use L-BFGS-B method. GPU is not supported.
    use_jax_scipy (bool, optional): whether to use jax.scipy.optimize.minimize for TT-sweep.
        Defaults to False. This optimizer is only supports BFGS method, which exhausts GPU memory.
    method (str, optional): the optimization method for scipy.optimize.minimize.
        Defaults to 'L-BFGS-B'. Note that jax.scipy.optimize.minimize only supports 'BFGS'.
    ord (str, optional): the norm for scaling the initial core. 
        Defaults to 'fro', Frobenuis norm.
        'max`, maximum absolute value, 'fro', Frobenius norm, are supported.
    auto_onedot (bool, optional): whether to switch to one-dot core optimization automatically once
        the maximum rank is reached. Defaults to True.
        This will cause overfitting in the beginning of the optimization.
File:      ~/GitHub/Pompon/pompon/optimizer/sweeper.py
Type:      function

norm, W = get_norm_W(tt)
basis = model.basis(x_samples)
basis[0].shape

(256, 2)

y_samples.shape

(256, 1)

sweep(
    tt=tt,
    basis=basis,
    y=y_samples,
    nsweeps=2,
    maxdim=2,
    opt_maxiter=100,
    optax_solver=optax.adam(1.0e-03),
    # use_CG=True,
    onedot=False,
    auto_onedot=False,
)

Repeat tensor train optimization & basis optimization

tx = optax.adam(1e-5)
optimizer = nnx.Optimizer(model, tx)

for i in tqdm(range(10000)):
    if i % 500 == 0:
        norm, W = get_norm_W(tt)
        basis = model.basis(x_samples)
        sweep(
            tt=tt,
            basis=basis,
            y=y_samples,
            nsweeps=1,
            maxdim=2,
            opt_maxiter=200,
            # optax_solver=optax.adam(1.e-04),
            use_CG=True,
            onedot=False,
            auto_onedot=False,
        )
        norm, W = get_norm_W(tt)
    loss = train_step(model, optimizer, x_samples, y_samples, W, norm)
    losses.append(loss)

show_trace(losses)

show_basis(model, tt)

Train with forces

Train basis with fixed tensor-train

Define function that returns \(-\frac{\partial V}{\partial x}\) by auto differentiation

from functools import partial


def get_force(x, model, norm, W):
    def func(x, model, norm, W):
        if x.ndim == 1:
            # When no-batch
            x = x[jnp.newaxis, :]
            return -1.0 * model(x, norm=norm, W=W).squeeze(0)
        else:
            return -1.0 * model(x, norm=norm, W=W)

    ener_fn = partial(func, model=model, norm=norm, W=W)
    jacobian = jax.vmap(jax.jacrev(ener_fn))(x)  # (batch, out, in)
    return jacobian.squeeze(-2)  # (batch, in)

Define train_step which has a loss function \[ \mathcal{L} = \frac{1}{2|\mathcal{D}|} \sum_{\boldsymbol{x}, E, \boldsymbol{F} \in \mathcal{D}} \left[\left(\hat{V}(\boldsymbol{x})-V\right)^2 + \left(\hat{\mathbf{F}}(\boldsymbol{x})-\mathbf{F}\right)^2\right] \]

@nnx.jit
def train_step(model, optimizer, x, y, f, W, norm):
    def _loss_fn(model):
        pred = model(x, W, norm)
        loss = jnp.mean((pred - y) ** 2)
        pred_force = get_force(x, model, norm, W)
        loss += (
            jnp.sum((pred_force.flatten() - f.flatten()) ** 2)
            / pred_force.shape[0]
        )
        return loss

    loss, grads = nnx.value_and_grad(_loss_fn)(model)
    optimizer.update(grads)
    return loss

Check train_step works

norm, W = get_norm_W(tt)
loss = train_step(model, optimizer, x_samples, y_samples, f_samples, W, norm)
loss

Array(0.38388169, dtype=float64)

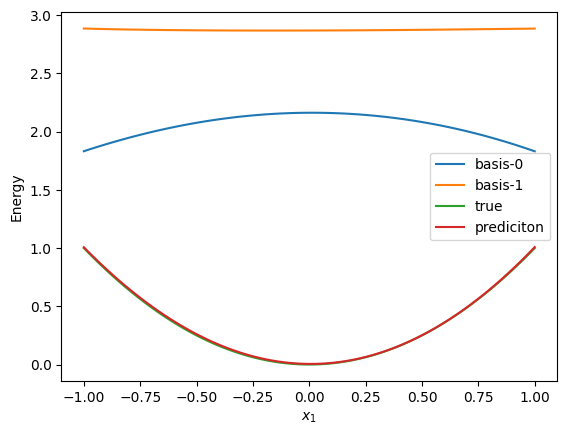
Train basis iteratively

for _ in tqdm(range(1000)):
    # lax while loop may be fast
    loss = train_step(
        model, optimizer, x_samples, y_samples, f_samples, W, norm
    )
    losses.append(loss)

show_trace(losses)

show_basis(model, tt)

Train tensor train with fixed basis

Prepare basis gradient \(-\frac{\partial \Phi}{\partial x_i}\)

def get_partial_basis(x, i, model):
    assert x.ndim == 2  # batch, dim
    x = x[:, i : i + 1]

    def func(x, model):
        if x.ndim == 1:
            x = x[jnp.newaxis, :]
            return -1.0 * model.basis(x, i)[0].squeeze(0)
        else:
            return -1.0 * model.basis(x, i)[0]

    basis_fn = partial(func, model=model)
    # since in=1 < out=number of basis, we should use forward differentiation
    jacobian = jax.vmap(jax.jacfwd(basis_fn))(x)  # batch, out, in
    return jacobian.squeeze(2)  # batch, out


partial_basis_i = get_partial_basis(x_samples, 0, model)

partial_basis= $ $

partial_basis = [
    get_partial_basis(x_samples, i, model) for i in range(x_samples.shape[1])
]

basis= \(\left[\phi_{\rho_1}, \phi_{\rho_2}, \cdots, \phi_{\rho_n} \right]\)

basis = model.basis(x_samples)

concat_y=\(y_p\) where \(p=k \otimes i\) \[ y_p = y_i^{(k)} = \begin{cases} \boldsymbol{F}_i^{(k)} & \mathrm{for} \quad i \leq n \\ E^{(k)} & \mathrm{for} \quad i = n+1 \end{cases} \]

concat_y = jnp.vstack(
    [f_samples[:, i : i + 1] for i in range(len(basis))] + [y_samples]
)
print(concat_y.shape)

(1024, 1)

basis_list= \[ \begin{bmatrix} [\partial_{x_1}\phi_{\rho_1} & \phi_{\rho_2} & \cdots & \phi_{\rho_n} ], \\ [\phi_{\rho_1} & \partial_{x_2}\phi_{\rho_2} & \cdots & \phi_{\rho_n} ], \\ & & \vdots & & \\ [\phi_{\rho_1} & \phi_{\rho_2} & \cdots & \partial_{x_n}\phi_{\rho_n} ], \\ [\phi_{\rho_1} & \phi_{\rho_2} & \cdots & \phi_{\rho_n} ] \end{bmatrix} \]

concat_basis= $ $ where \[ \varphi_{\rho_j}^p = \varphi_{i, \rho_i}^{(k)} = \begin{cases} -\partial_{x_j}\phi_{\rho_j} & \mathrm{for} \quad i=j \\ \phi_{\rho_j} & \mathrm{otherwise} \end{cases} \]

def get_concat_basis(x: jax.Array, model: CustomModel) -> list[jax.Array]:
    """
    Args:
        x (jax.Array): postions
        model (CustomModel): model

    Returns:
        list[jax.Array]: derivative concatenated basis
    """
    partial_basis = [get_partial_basis(x, i, model) for i in range(x.shape[1])]
    basis = model.basis(x)
    basis_list = []
    for i in range(len(basis)):
        basis_row = [
            ϕ.copy() if k != i else dϕ.copy()
            for k, (ϕ, dϕ) in enumerate(zip(basis, partial_basis, strict=True))
        ]
        basis_list.append(basis_row)
    basis_list.append(basis)
    concat_basis = [
        jnp.vstack([φ[i] for φ in basis_list]) for i in range(len(basis))
    ]
    return concat_basis


concat_basis = get_concat_basis(x_samples, model)
print(concat_basis[0].shape)

(1024, 2)

Train tensor train with fixed basis

Only basis & y are changed from energy optimization.

sweep(
    tt=tt,
    basis=concat_basis,  # <- changed!!
    y=concat_y,  # <- changed!!
    nsweeps=10,
    maxdim=2,
    opt_maxiter=200,
    # optax_solver=optax.adam(1.e-04),
    use_CG=True,
    onedot=True,
    auto_onedot=False,
)

show_basis(model, tt)

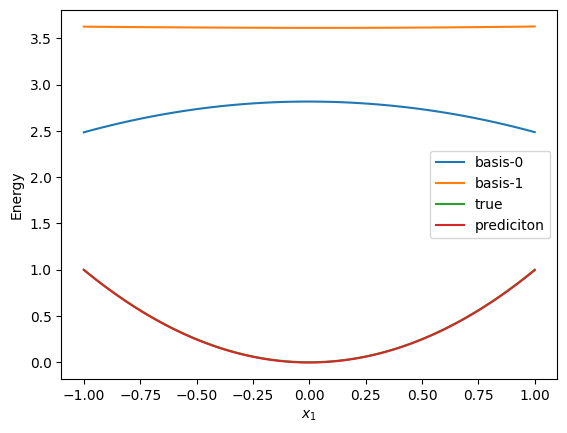
Repeat tensor train optimization & basis optimization

tx = optax.adam(1e-5)
optimizer = nnx.Optimizer(model, tx)
for i in tqdm(range(10000)):
    if i % 500 == 0:
        norm, W = get_norm_W(tt)
        concat_basis = get_concat_basis(x_samples, model)
        sweep(
            tt=tt,
            basis=concat_basis,
            y=concat_y,
            nsweeps=1,
            maxdim=2,
            opt_maxiter=200,
            # optax_solver=optax.adam(1.e-04),
            use_CG=True,
            onedot=True,
            auto_onedot=False,
        )
        norm, W = get_norm_W(tt)
    loss = train_step(
        model, optimizer, x_samples, y_samples, f_samples, W, norm
    )
    losses.append(loss)

show_trace(losses)

show_basis(model, tt)

Access optimized tensor train cores

for i, core in enumerate(tt):
    print(i, core)
    print(core.data)

0 Core(shape=(1, 2, 2), leg_names=('β0', 'i1', 'β1'), dtype=float64)
[[[-0.23738906 -0.24130501]
  [-0.93898443  0.06104555]]]
1 Core(shape=(2, 2, 2), leg_names=('β1', 'i2', 'β2'), dtype=float64)
[[[-0.58550331  0.05419654]
  [ 0.80821735  0.03214547]]

 [[-0.8099358  -0.07141367]
  [-0.57994308 -0.05069637]]]
2 Core(shape=(2, 2, 1), leg_names=('β2', 'i3', 'β3'), dtype=float64)
[[[-0.99307731]
  [ 0.11746261]]

 [[ 0.11746261]
  [ 0.99307731]]]