Convert NN-MPO to ITensor MPO

Code 
import matplotlib.pyplot as plt
import numpy as np
from discvar import HarmonicOscillator as HO

import pompon
import pompon.utils

Define harmonic frequencies

Code 
freqs = [1193.495, 1264.160, 1529.535, 1863.269, 2867.313, 2926.465]

Load trained NN-MPO

Code 
nnmpo = pompon.NNMPO.import_h5("data/nnmpo_final_rmse_8.365e-04.h5")
nnmpo.rescale(1.0, 1 / 27.21138)  # eV to Eh
2024-10-18 16:14:49 - INFO:pompon.pompon.model - Model is imported from data/nnmpo_final_rmse_8.365e-04.h5
Code 
U = np.array(nnmpo.coordinator.U.data)
plt.imshow(np.abs(U))
plt.colorbar()
plt.show()

\[ Q = \xi U \] \[ \frac12 \xi \begin{pmatrix} \omega_1 ^2 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \omega_f^2 \end{pmatrix} \xi^T = \frac12 Q U^T \begin{pmatrix} \omega_1 ^2 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \omega_f^2 \end{pmatrix} U Q^T \]

Code 
latent_freqs = np.sqrt(np.diag((U.T @ np.diag(np.array(freqs) ** 2) @ U)))
print(latent_freqs)
[1193.51968001 1265.06644987 1532.43704947 1861.63527484 2867.18137401
 2925.71361408]

Define wavefunction basis

basis = \(\left[|\sigma_1\rangle, |\sigma_2\rangle, \cdots, |\sigma_6\rangle\right]\)

Code 
N = 9
basis = [HO(ngrid=N, omega=omega, units="cm-1") for omega in latent_freqs]

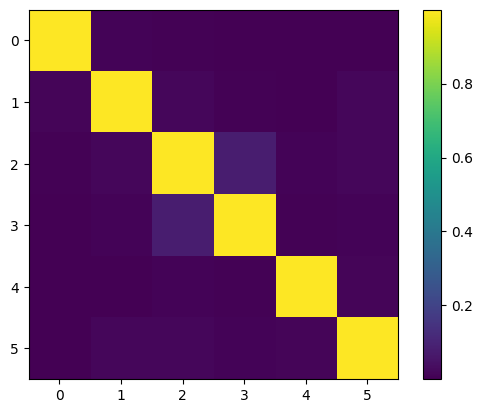
Evaluate one-dimensional integral

basis_ints=\(\left[\langle\sigma_1|\phi_{\rho_1}|\sigma_1\rangle, \langle\sigma_2|\phi_{\rho_2}|\sigma_2\rangle, \cdots, \langle\sigma_6|\phi_{\rho_6}|\sigma_6\rangle\right]\)

Note that off-diagnal terms are approximated to 0 by DVR.

Code 
basis_ints = [
    getattr(nnmpo.basis, f"phi{i}").forward(
        np.array(basis[i].get_grids()), nnmpo.q0[:, i]
    )
    for i in range(6)
]
delta = np.eye(N, N)
basis_ints_full = [
    np.einsum("ij,ik->ijk", basis_ints[i], delta) for i in range(6)
]

Conversion

Code 
mpo = nnmpo.convert_to_mpo(basis_ints_full)
for core in mpo:
    print(core.shape)
(1, 9, 9, 5)
(5, 9, 9, 14)
(14, 9, 9, 14)
(14, 9, 9, 14)
(14, 9, 9, 6)
(6, 9, 9, 1)

Define Kinetic MPO

KEO-MPO can be encoded into \[ \begin{pmatrix} \frac{-\hat{P}_1^2}{2} & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ \frac{-\hat{P}_2^2}{2} & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ \frac{-\hat{P}_3^2}{2} & 1 \end{pmatrix} \begin{pmatrix} 1 \\ \frac{-\hat{P}_4^2}{2} \end{pmatrix} \]

Code 
kinetic_mpo = (
    [np.zeros((1, N, N, 2))]
    + [np.zeros((2, N, N, 2)) for _ in range(4)]
    + [np.zeros((2, N, N, 1))]
)
for idof in range(6):
    op = basis[idof].get_2nd_derivative_matrix_dvr().real * -1 / 2
    eye = np.eye(basis[idof].ngrid)
    if idof == 0:
        kinetic_mpo[idof][0, :, :, 0] = op
        kinetic_mpo[idof][0, :, :, 1] = eye
    elif idof == 5:
        kinetic_mpo[idof][0, :, :, 0] = eye
        kinetic_mpo[idof][1, :, :, 0] = op
    else:
        kinetic_mpo[idof][0, :, :, 0] = eye
        kinetic_mpo[idof][1, :, :, 1] = eye
        kinetic_mpo[idof][1, :, :, 0] = op

Merge KEO and PEO and save as itensor

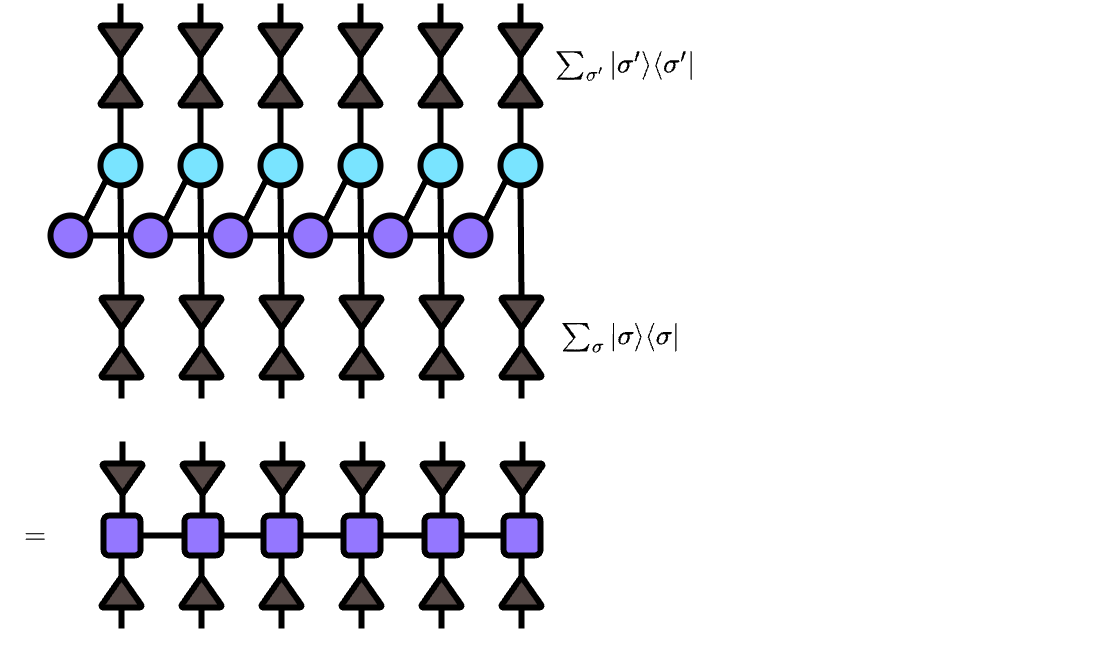
\[ \sum_{\{\beta\}} V\substack{\sigma_1^\prime \\ 1 \beta_1 \\ \sigma_1} V\substack{\sigma_2^\prime \\ \beta_1 \beta_2 \\ \sigma_2} \cdots V\substack{\sigma_6^\prime \\ \beta_5 1 \\ \sigma_6} + \sum_{\{\gamma\}} T\substack{\sigma_1^\prime \\ 1 \gamma_1 \\ \sigma_1} T\substack{\sigma_2^\prime \\ \gamma_1 \gamma_2 \\ \sigma_2} \cdots T\substack{\sigma_6^\prime \\ \gamma_5 1 \\ \sigma_6} = \sum_{\{\alpha\}} H\substack{\sigma_1^\prime \\ 1 \alpha_1 \\ \sigma_1} H\substack{\sigma_2^\prime \\ \alpha_1 \alpha_2 \\ \sigma_2} \cdots H\substack{\sigma_6^\prime \\ \alpha_5 1 \\ \sigma_6} \]

where \[ H\substack{\sigma_1^\prime \\ 1 \alpha_1 \\ \sigma_1} = \begin{pmatrix} V\substack{\sigma_1^\prime \\ 1 \beta_1 \\ \sigma_1} & T\substack{\sigma_1^\prime \\ 1 \gamma_1 \\ \sigma_1} \end{pmatrix}, H\substack{\sigma_2^\prime \\ \alpha_1 \alpha_2 \\ \sigma_2} = \begin{pmatrix} V\substack{\sigma_2^\prime \\ \beta_1 \beta_2 \\ \sigma_2} & 0 \\ 0 & T\substack{\sigma_2^\prime \\ \gamma_1 \gamma_2 \\ \sigma_2} \end{pmatrix}, \cdots, H\substack{\sigma_6^\prime \\ \alpha_5 1 \\ \sigma_6} = \begin{pmatrix} V\substack{\sigma_6^\prime \\ \beta_5 1 \\ \sigma_6} \\ T\substack{\sigma_6^\prime \\ \gamma_5 1 \\ \sigma_6} \end{pmatrix} \] and \(\alpha_i = \beta_i \oplus \gamma_i\)

Code 
new_mpo = []
for i in range(6):
    m0, n1, np1, m1 = mpo[i].shape
    M0, N1, Np1, M1 = kinetic_mpo[i].shape
    assert n1 == np1 == N1 == Np1
    if i == 0:
        assert m0 == M0 == 1
        new_core = np.zeros((1, n1, n1, m1 + M1))
        new_core[:, :, :, :m1] = mpo[i]
        new_core[:, :, :, m1:] = kinetic_mpo[i]
    elif i == 5:
        assert m1 == M1 == 1
        new_core = np.zeros((m0 + M0, n1, n1, 1))
        new_core[:m0, :, :, :] = mpo[i]
        new_core[m0:, :, :, :] = kinetic_mpo[i]
    else:
        new_core = np.zeros((m0 + M0, n1, n1, m1 + M1))
        new_core[:m0, :, :, :m1] = mpo[i]
        new_core[m0:, :, :, m1:] = kinetic_mpo[i]
    new_mpo.append(new_core)
pompon.utils.export_mpo_to_itensor(new_mpo, "random-mpo.h5", "H") 
# random-mpo.h5 must be prepared in advance. See also create-random-mpo.ipynb
'random-mpo_filled.h5'
Code 
!cp random-mpo_filled.h5 nnmpo-ham.h5
/opt/homebrew/Cellar/python@3.12/3.12.2_1/Frameworks/Python.framework/Versions/3.12/lib/python3.12/pty.py:95: RuntimeWarning: os.fork() was called. os.fork() is incompatible with multithreaded code, and JAX is multithreaded, so this will likely lead to a deadlock.
  pid, fd = os.forkpty()